题目内容
 如图所示,静止在匀强磁场中的,
如图所示,静止在匀强磁场中的,6 3 |
6 3 |
1 0 |
3 1 |
4 2 |
(1)
3 1 |
(2)在图中画出粒子
3 1 |
4 2 |
(3)当粒子
4 2 |
3 1 |
分析:(1)由动量守恒求得速度的大小与方向.(2)由R=
求得R之比.(3)由周期T=
求得周期之比,再求得旋转周数.
| mv |
| Bq |
| 2πm |
| Bq |
解答:解:(1)36Li核俘获 01n的过程,系统动量守恒,则mHv0=mHv1+mHev2,即v1=
代入数据mn=1 u,mHe=4 u,mH=3 u,得v1=-1.0×103 m/s,负号表示跟v0的方向相反.
(2)运动轨迹如图所示 13H和 24He在磁场中半径之比为 rH:rHe=
:
=3:40
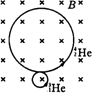
(3)H和 He的周期之比为TH:THe=
:
=3:2
所以它们的转动周期之比为nH:nHe=THe:TH=2:3 当 α粒子转3周时,氘核转动2周.
答:(1)13H的速度是-1.0×103 m/s.
(2)它们的轨道半径之比:3:40.
(3)粒子13H旋转2周.
| mnv0- mHev2 |
| mH |
代入数据mn=1 u,mHe=4 u,mH=3 u,得v1=-1.0×103 m/s,负号表示跟v0的方向相反.
(2)运动轨迹如图所示 13H和 24He在磁场中半径之比为 rH:rHe=
| mHv1 |
| Bq1 |
| mHev2 |
| Bq2 |

(3)H和 He的周期之比为TH:THe=
| 2πnH |
| Bq1 |
| 2 πnHe |
| Bq2 |
所以它们的转动周期之比为nH:nHe=THe:TH=2:3 当 α粒子转3周时,氘核转动2周.
答:(1)13H的速度是-1.0×103 m/s.
(2)它们的轨道半径之比:3:40.
(3)粒子13H旋转2周.
点评:由半径公式分析半径之比的决定物理量,由周期公式分析周期之比的决定物理量,进而求得旋转周数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010?湖南模拟)如图所示,静止在匀强磁场中的
(2010?湖南模拟)如图所示,静止在匀强磁场中的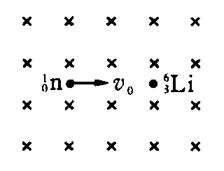 若已知核反应后
若已知核反应后
