��Ŀ����
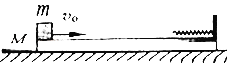
����Ŀ����ͼ������ֱƽ���ڣ��뾶ΪR�İ�Բ�ι��CDE��ˮƽ���AC���⻬����������C�㣮ˮƽ���AC����һ���ʵ��ɣ�������������ڹ̶��ĵ����ϣ��������ɶ�B��C��ľ���Ϊ4R������һ��С����ѹ������˨�ӣ��������ɵĵ�������ΪEP1ʱ����С���ɾ�ֹ�ͷţ�С��ǡ����ͨ����Բ�ι������ߵ�E��֮���ٴ��ø�С��ѹ�����ɣ������ɵĵ�������ΪEP2ʱ����С���ɾ�ֹ�ͷţ�С��BCDE����׳���ǡ������B�㣬����ʼ�մ��ڵ������ڣ���
��1����һ��ѹ�����ɣ��ͷ�С���С����ߵ�Eʱ���ٶȴ�С��
��2����������EP1��EP2֮�ȣ�
���𰸡�
��1���⣺��һ��ѹ�����ɣ���С������ߵ�Eʱ���ٶ�Ϊv1�����ٽ�������֪��mg=m ![]()
�ã�v1= ![]()
�𣺵�һ��ѹ�����ɣ��ͷ�С���С����ߵ�Eʱ���ٶȴ�С�� ![]() ��
��
��2���⣺��һ��ѹ���ͷ�С����ɻ�е���غ㶨�ɿɵã�
Ep1=mg��2R+ ![]()
���ϼ�ʽ������ã�Ep1= ![]() mgR
mgR
�ڶ���ѹ��ʱС��ͨ����ߵ�Eʱ���ٶ�Ϊv2���ɻ�е���غ㶨�ɿɵã�
Ep2=mg2R+ ![]()
���E�㿪ʼ��ƽ���˶�����ƽ���˶����ɵã�
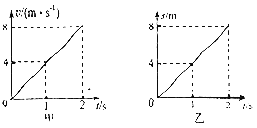
4R=v2t��R= ![]() gt2
gt2
��� v2=2 ![]() Ep2=4mgR
Ep2=4mgR
�� EP1��EP2=5��8
�𣺵�������EP1��EP2֮��5��8��
����������1������������Բ���˶����������ֱƽ����ߵ���ٽ����� �����һ��ѹ�����ɣ��ͷ�С���С����ߵ�Eʱ���ٶȡ�
��2����������ѹ��С����˶�����ж����λ�е�ܶ��غ㣬�ٽ��ƽ���˶��Ĺ��ɽ�����⡣
�����㾫����������Ĺؼ���������ƽ���˶������֪ʶ�������ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶����Լ��������������⣬�˽�����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������