题目内容
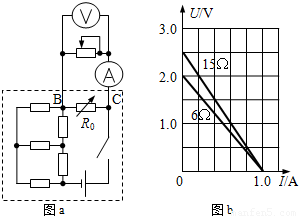
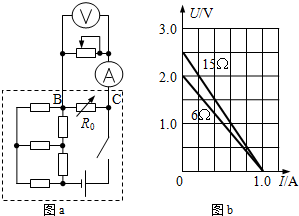 如图a所示,虚线框内为某个复杂电路,其中接在BC两点间的R0是电阻箱.某同学利用滑动变阻器、电流表和电压表研究该电路中BC两点间的电压与电流关系.其步骤如下:
如图a所示,虚线框内为某个复杂电路,其中接在BC两点间的R0是电阻箱.某同学利用滑动变阻器、电流表和电压表研究该电路中BC两点间的电压与电流关系.其步骤如下:①调节R0到某个数值,闭合电键.
②移动滑动变阻器滑片,得到两电表的多组读数;
③作U-I图象;
每次都调节不同的R0,在重复多次实验后,发现得到的U-I图象都是直线,该同学将其中R0=15Ω、R0=6Ω两条图象延长与坐标轴相交,如图b所示.
(1)多条U-I图象都与I轴交于同一点,与R0取值无关.试简述其原因:
(2)当R0=15Ω、滑动变阻器阻值为10Ω时,滑动变阻器消耗的功率为
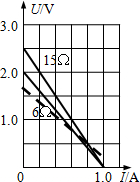
(3)在图b中作出R0=3Ω时的U-I的图象.
分析:(1)此时电阻箱被短路,短路电流与电阻箱阻值无关;
(2)当R0=15Ω时,虚线框内部相当与电源,通过图象求出电动势和内电阻,再结合闭合电路欧姆定律求解出电流,然后求解外接电阻的功率;
(3)求出实际电源的电动势和虚线框内除去电阻箱以外的其余部分的总电阻,然后求解出接入R0=3Ω时的短路电流和断路时的路端电压,在U-I图象中描点后连成直线即可.
(2)当R0=15Ω时,虚线框内部相当与电源,通过图象求出电动势和内电阻,再结合闭合电路欧姆定律求解出电流,然后求解外接电阻的功率;
(3)求出实际电源的电动势和虚线框内除去电阻箱以外的其余部分的总电阻,然后求解出接入R0=3Ω时的短路电流和断路时的路端电压,在U-I图象中描点后连成直线即可.
解答:解:(1)滑动变阻器被短路;
当U=0时,滑动变阻器R0被局部短路,阻值对电路没有影响,所以电流都相同.
故答案为:当U=0时,滑动变阻器R0被局部短路,阻值对电路没有影响.
(2)虚线框内部相当与电源,由图象可以得到,电动势E=2.5V,内阻r=|
|=
=2.5Ω
根据闭合电路欧姆定律,电流为I=
=
=0.1A
动变阻器消耗的功率P=I2R=(0.1A)2×10Ω=0.1W
故答案为:0.1W.
(3)设实际电源的电动势为E0,虚线框内除去电阻箱以外的其余部分的总电阻为R1,根据闭合电路欧姆定律,有
U=E0-IR1=
代入数据
0=E0-1×R1(短路)
2.5=
(R0=15Ω,断路时)
解得
E0=3V,R1=3Ω
当R0=3Ω时,短路电路为1.0A;
断路时路端电压为U=E=
=
=1.5V
在图b中作出R0=3Ω时的U-I的图象,如图.(截距为1.5V,经过(1,0)直线)
当U=0时,滑动变阻器R0被局部短路,阻值对电路没有影响,所以电流都相同.
故答案为:当U=0时,滑动变阻器R0被局部短路,阻值对电路没有影响.
(2)虚线框内部相当与电源,由图象可以得到,电动势E=2.5V,内阻r=|
| △U |
| △I |
| 2.5-0 |
| 1,0-0 |
根据闭合电路欧姆定律,电流为I=
| E |
| R0+R |
| 2.5V |
| 15Ω+10Ω |
动变阻器消耗的功率P=I2R=(0.1A)2×10Ω=0.1W
故答案为:0.1W.
(3)设实际电源的电动势为E0,虚线框内除去电阻箱以外的其余部分的总电阻为R1,根据闭合电路欧姆定律,有
U=E0-IR1=
| R0E0 |
| R1+R0 |
代入数据
0=E0-1×R1(短路)
2.5=
| 15E0 |
| R1 +15 |
解得
E0=3V,R1=3Ω
当R0=3Ω时,短路电路为1.0A;
断路时路端电压为U=E=
| R0E0 |
| R1+R0 |
| 3×3 |
| 3+3 |
在图b中作出R0=3Ω时的U-I的图象,如图.(截距为1.5V,经过(1,0)直线)

点评:本题是测量有源二端网络的电动势和内电阻的问题,可以将有源二端网络等效成一个电源,电源电动势等于断路时的路段电压.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
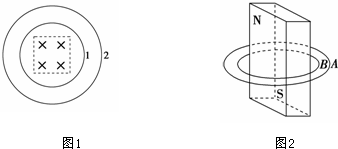
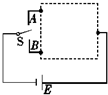 在如图甲所示的虚线框中有一种发热装置,它是由三段阻值相同的电热丝组成的.这个发热装置的电路与虚线框外的电路相连接,当开关S扳到A点时为高温,扳到B点时为低温(电源的路端电压不变),且在相同时间内,高温时产生的热量是低温时产生热量的2倍.试在虚线框内画出该装置内的电路图.
在如图甲所示的虚线框中有一种发热装置,它是由三段阻值相同的电热丝组成的.这个发热装置的电路与虚线框外的电路相连接,当开关S扳到A点时为高温,扳到B点时为低温(电源的路端电压不变),且在相同时间内,高温时产生的热量是低温时产生热量的2倍.试在虚线框内画出该装置内的电路图.