题目内容
2.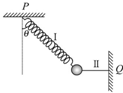 如图所示,质量为m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小为FT1,Ⅱ中拉力大小为FT2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )
如图所示,质量为m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小为FT1,Ⅱ中拉力大小为FT2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )| A. | 若断Ⅰ,则a=g,竖直向下 | |
| B. | 若断Ⅱ,则a=g,竖直向上 | |
| C. | 若断Ⅱ,则a=$\frac{{F}_{{T}_{2}}}{m}$,方向水平向左 | |
| D. | 若断Ⅰ,则a=$\frac{{F}_{{T}_{1}}}{m}$,方向沿Ⅰ的延长线 |
分析 先研究原来静止的状态,由平衡条件求出弹簧和细线的拉力.刚剪短细绳时,弹簧来不及形变,故弹簧弹力不能突变;细绳的形变是微小形变,在刚剪短弹簧的瞬间,细绳弹力可突变!根据牛顿第二定律求解瞬间的加速度.
解答 解:AD、绳子未断时,受力如图,由共点力平衡条件得:
FT2=mgtanθ,${F}_{T1}=\frac{mg}{sinθ}$刚剪断弹簧Ⅰ瞬间,细绳弹力突变为0,故小球只受重力,加速度为g,竖直向下,故A正确,D错误;
BC、刚剪短细线瞬间,弹簧弹力和重力不变,受力如图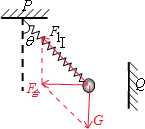
由几何关系,F合=FT1sinθ=FFT2=ma,因而a=$\frac{{F}_{1}sinθ}{m}$=$\frac{{F}_{T2}}{m}$方向水平向左,故C正确,B错误.
故选:AC
点评 本题为瞬时问题,关键要抓住弹簧弹力不可突变,细绳弹力可突变!

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.关于第一宇宙速度,下列说法错误的是( )
| A. | 它是人造地球卫星绕地球作匀速圆周运动的最大速度 | |
| B. | 它是人造地球卫星在圆形轨道上的最小运行速度 | |
| C. | 它是能使卫星绕地球运行的最大发射速度 | |
| D. | 它是人造卫星绕地球作椭圆轨道运行时在近地点的速度 |
13.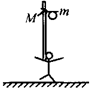 如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M的竖直竹竿,竿上有一质量为m的人可以看成质点,当此人沿着竖直竿以加速度a加速下滑时,竿对地面上的人的压力大小为( )
如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M的竖直竹竿,竿上有一质量为m的人可以看成质点,当此人沿着竖直竿以加速度a加速下滑时,竿对地面上的人的压力大小为( )
 如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M的竖直竹竿,竿上有一质量为m的人可以看成质点,当此人沿着竖直竿以加速度a加速下滑时,竿对地面上的人的压力大小为( )
如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M的竖直竹竿,竿上有一质量为m的人可以看成质点,当此人沿着竖直竿以加速度a加速下滑时,竿对地面上的人的压力大小为( )| A. | (M+m)g+ma | B. | (M+m)g-ma | C. | (M+m)g | D. | (M-m)g |
17. 如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )
如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )
 如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )
如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )| A. | 增大两板间电势差U2 | B. | 尽可能使板长l短一些 | ||
| C. | 尽可能使板距d小一些 | D. | 使加速电压U1升高一些 |
5.一个点电荷从静电场中的A点移到电场中的B点,其电势能变化为零,则( )
| A. | A、B两点处的场强一定相等 | |
| B. | 该电荷一定能够沿着某一等势面移动 | |
| C. | A、B两点的电势一定相等 | |
| D. | 作用于该电荷上的电场力始终与其运动方向垂直 |
6. 如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )
如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )
 如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )
如图所示,一理想变压器的原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,电阻R=8.8Ω,原线圈接入一电压u=220$\sqrt{2}$sin100πt(V)的交流电源,交流电压表和交流电流表均为理想电表,则( )| A. | 副线圈交变电流的频率是100 Hz | B. | t=1s的时刻,电压表的示数为0 | ||
| C. | 变压器的输入电功率为220W | D. | 电流表的示数为$5\sqrt{2}$A |
 直角钢尺AOB的O 处为一光滑的水平轴,OA段长1米,质量为2千克,OB段长0.5米,质量为3千克(已知OA段、OB段的质量都是均匀分布),当钢尺静止时,OA段与竖直线所成的夹角为37°,现用手托住A端缓慢地抬起钢尺使OA段水平,在此过程中人对钢尺做的功为5 焦.
直角钢尺AOB的O 处为一光滑的水平轴,OA段长1米,质量为2千克,OB段长0.5米,质量为3千克(已知OA段、OB段的质量都是均匀分布),当钢尺静止时,OA段与竖直线所成的夹角为37°,现用手托住A端缓慢地抬起钢尺使OA段水平,在此过程中人对钢尺做的功为5 焦.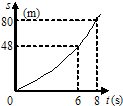 如图所示,为一物体的s-t图象,它是一抛物线,从图象中可以判定物体作匀加速直线运动,物体在8s内的位移是80m,物体运动48m所经历的时间是6s,物体在第7s末的瞬时速度大小是16m/s.
如图所示,为一物体的s-t图象,它是一抛物线,从图象中可以判定物体作匀加速直线运动,物体在8s内的位移是80m,物体运动48m所经历的时间是6s,物体在第7s末的瞬时速度大小是16m/s.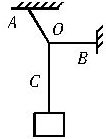 如图所示,三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物.其中细绳OB是水平的,A端、B端固定.若逐渐增加C端所挂物体的质量,试判断那段绳子先断?
如图所示,三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物.其中细绳OB是水平的,A端、B端固定.若逐渐增加C端所挂物体的质量,试判断那段绳子先断?