题目内容
16.在做“研究匀变速直线运动”的实验时,某同学得到一条用电火花计时器打下的纸带如图2所示,并在其上取了A、B、C、D、E、F、G 7个计数点,每相邻两个计数点间还有4个点图中没有画出,电火花计时器接220V、50Hz交流电源.
(1)打点计时器每0.02s打一个点.
(2)设电火花计时器的打点周期为T,计算F点的瞬时速度vF的公式为vF=$\frac{{d}_{6}-{d}_{4}}{2T}$;(用图中d1~d6及T表示)
(3)他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表.
| 对应点 | B | C | D | E | F |
| 速度(m/s) | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
(4)如果当时电网中交变电流的电压变成210V,而做实验的同学并不知道,那么加速度的测量值与实际值相比不变.(填“偏大”、“偏小”或“不变”)
(5)小进同学根据课本38页介绍,将自己实验得到的纸带,按相等的时间间隔取连续的几段位移,从它们的分界点将纸带剪断,剪得的几段纸带按图4所示的顺序贴在坐标中,各段紧靠但不重叠,得到图5所示的直方图.根据这个直方图他可求出加速度.

分析 打点计时器的打点频率是与交流电源的频率相同,所以即使电源电压降低也不改变打点计时器打点周期.
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上F点时小车的瞬时速度大小,根据速度-时间图象的斜率表示加速度解出加速度的数值,
解答 解:(1)打点计时器的周期T=$\frac{1}{f}=\frac{1}{50}=0.02s$,
(2)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度得:${v}_{F}=\frac{{x}_{EG}}{2T}=\frac{{d}_{6}-{d}_{4}}{2T}$
(3)根据(1)中得到的数据,以A点对应的时刻为t=0,作出v-t图象,如图所示:
由速度-时间图象的斜率表示加速度,得:a=$\frac{0.3-0.1}{0.5}$m/s2=0.40m/s2
(5)电网电压变化,并不改变打点的周期,故测量值与实际值相比不变.
(6)所选纸带时间间隔相等,故可以等效代替速度;
故图象纵坐标名称为速度;横坐标为时间,本段时间内的平均速度表示中间时刻的瞬时速度,故将各段中点用直线相连,即为v-t图象,如图所示;

v-t图线中,图象的斜率就是加速度.故可以求出斜率来表示加速度.
故答案为:(1)0.02; (2)$\frac{{d}_{6}-{d}_{4}}{2T}$;(3)0.40;(4)不变;(5)加速度.
点评 要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

练习册系列答案
相关题目
6.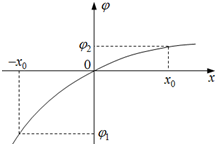 某静电场中有一条电场线与x轴重合,纵轴ϕ表示该条电场线上对应各点的电势,ϕ随x的变化规律如图曲线所示.x轴上坐标为x1=-x0点的电势和电场强度大小分别为ϕ1和E1,坐标x2=x0点的电势和电场强度大小分别为ϕ2和E2,下列有关判断正确的是( )
某静电场中有一条电场线与x轴重合,纵轴ϕ表示该条电场线上对应各点的电势,ϕ随x的变化规律如图曲线所示.x轴上坐标为x1=-x0点的电势和电场强度大小分别为ϕ1和E1,坐标x2=x0点的电势和电场强度大小分别为ϕ2和E2,下列有关判断正确的是( )
 某静电场中有一条电场线与x轴重合,纵轴ϕ表示该条电场线上对应各点的电势,ϕ随x的变化规律如图曲线所示.x轴上坐标为x1=-x0点的电势和电场强度大小分别为ϕ1和E1,坐标x2=x0点的电势和电场强度大小分别为ϕ2和E2,下列有关判断正确的是( )
某静电场中有一条电场线与x轴重合,纵轴ϕ表示该条电场线上对应各点的电势,ϕ随x的变化规律如图曲线所示.x轴上坐标为x1=-x0点的电势和电场强度大小分别为ϕ1和E1,坐标x2=x0点的电势和电场强度大小分别为ϕ2和E2,下列有关判断正确的是( )| A. | ϕ1>ϕ2,E1>E2 | B. | ϕ1<ϕ2,E1>E2 | C. | ϕ1>ϕ2,E1<E2 | D. | ϕ1<ϕ2,E1<E2 |
7.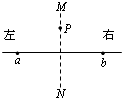 图中a、b是两个点电荷,它们的电量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上的一点.下列哪中情况能使P点场强方向指向MN的左侧( )
图中a、b是两个点电荷,它们的电量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上的一点.下列哪中情况能使P点场强方向指向MN的左侧( )
 图中a、b是两个点电荷,它们的电量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上的一点.下列哪中情况能使P点场强方向指向MN的左侧( )
图中a、b是两个点电荷,它们的电量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上的一点.下列哪中情况能使P点场强方向指向MN的左侧( )| A. | Q1、Q2都是正电荷,且Q1>Q2 | B. | Q1是正电荷,Q2是负电荷,且Q1>|Q2| | ||
| C. | Q1是负电荷,Q2是正电荷,且|Q1|>Q2 | D. | Q1、Q2都是负电荷,且|Q1|<|Q2| |
4.在美国尤金举行的2015年国际田联钻石联赛尤金站比赛中,中国飞人苏炳添在男子100米比赛中,以9秒99的成绩获得季军.苏炳添就此成为历史上首位突破10秒大关的亚洲人,他到达终点时的速度为12m/s,则他全程的平均速度大小约( )
| A. | 6m/s | B. | 11m/s | C. | 10m/s | D. | 12m/s |
11.下列说法,正确的是( )
| A. | 两个物体之间只要有摩擦力就一定会有弹力 | |
| B. | 滑动摩擦力的方向总是和物体的运动方向相反 | |
| C. | 形状规则的物体的重心与其几何中心重合 | |
| D. | 放在桌面上的物体受到的支持力是由于桌面发生弹性形变而产生的 |
5. 一质点做匀变速直线运动,如图所示,途中依次通过a、b、c三点,已知tab=tbc,若ac段的平均速度为v1,b点的瞬时速度为v2,则( )
一质点做匀变速直线运动,如图所示,途中依次通过a、b、c三点,已知tab=tbc,若ac段的平均速度为v1,b点的瞬时速度为v2,则( )
 一质点做匀变速直线运动,如图所示,途中依次通过a、b、c三点,已知tab=tbc,若ac段的平均速度为v1,b点的瞬时速度为v2,则( )
一质点做匀变速直线运动,如图所示,途中依次通过a、b、c三点,已知tab=tbc,若ac段的平均速度为v1,b点的瞬时速度为v2,则( )| A. | v1>v2 | B. | v1=v2 | C. | v1<v2 | D. | 无法确定 |
6. 如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )
如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )
 如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )
如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )| A. | 摩擦力对物块所做的功为mglsinθ(1-cosθ) | |
| B. | 弹力对物块所做的功为mglsinθcosθ | |
| C. | 木板对物块所做的功为mglsinθ | |
| D. | 合力对物块所做的功为mglcosθ |
