题目内容
【题目】为提高冰球运动员的加速能力,教练员在冰面上与起跑线距离s0和s1(s1<s0)处分别设置一个挡板和一面小旗,如图所示.训练时,让运动员和冰球都位于起跑线上,教练员将冰球以速度v0击出,使冰球在冰面上沿垂直于起跑线的方向滑向挡板:冰球被击出的同时,运动员垂直于起跑线从静止出发滑向小旗.训练要求当冰球到达挡板时,运动员至少到达小旗处.假定运动员在滑行过程中做匀加速运动,冰球到达挡板时的速度为v1 . 重力加速度为g.求
(1)冰球与冰面之间的动摩擦因数;
(2)满足训练要求的运动员的最小加速度.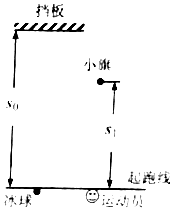
【答案】
(1)
解:对冰球分析,根据速度位移公式得: ![]() ,
,
加速度为:a= ![]() ,
,
根据牛顿第二定律得:a=μg,
解得冰球与冰面之间的动摩擦因数为: ![]() .
.
答:冰球与冰面之间的动摩擦因数![]()
(2)
根据两者运动时间相等,有: ![]() ,
,
解得运动员到达小旗处的最小速度为:v2= ![]() ,
,
则最小加速度为: ![]() =
= ![]() .
.
答:满足训练要求的运动员的最小加速度为 ![]() .
.
【解析】(1)根据速度位移公式求出冰球的加速度,结合牛顿第二定律求出动摩擦因数的大小.
(2)抓住两者运动时间相等得出运动员到达小旗处的最小速度,结合速度位移公式求出最小加速度.

练习册系列答案
相关题目