题目内容
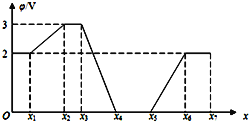
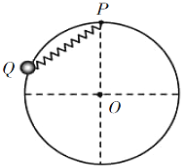
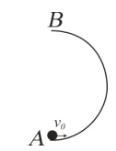
【题目】空间存在有一圆柱形的匀强磁场区域,其横截面如图1所示,磁感应强度随时间按照图2所示的规律均匀变化。图中B0和t0为已知量。

a.用电阻为R的细导线做成半径为r的圆环(图中未画出),圆环平面垂直于该磁场,圆环的中心与磁场中心重合。圆环半径小于该磁场的横截面半径。求t=t0时磁感应强度随时间的变化率![]() ,以及圆环中的电流。
,以及圆环中的电流。
b.上述导体圆环中产生的电流,实际是导体中的自由电荷在感生电场力的作用下做定向运动,而且自由电荷受到感生电场力的大小可以根据电动势的定义和法拉第电磁感应定律推导出来。现将导体圆环替换成一个用绝缘细管做成的半径为r的封闭圆形管道,且圆形管道的中心与磁场区域的中心重合(图中未画出)。管道内有一小球,小球质量为m,带电量为+q。忽略小球的重力和一切阻力。t=0时小球静止。求t=t0时小球的速度大小及管道对小球的弹力大小。
【答案】a. ![]()
![]() b.
b.![]()
![]()
【解析】
a、根据图2可求解△B/△t ,根据法拉第电磁感应定律和闭合电路欧姆定律列式求解感应电流大小;
b、根据法拉第电磁感应定律和电动势的定义求得感生电场的电场强度;在根据牛顿第二定律和运动学公式求解小球的速度大小及管道对小球的弹力大小。
a. 磁感应强度的变化率 ![]()
根据法拉第电磁感应定律,有:![]()
根据闭合电路欧姆定律有![]()
b.根据法拉第电磁感应定律有 ![]()
根据电动势定义有 ![]()
由上可得 ![]()
小球所受感生电场的作用力为![]()
在感生电场力的作用下,小球速度不断增加,将其转化为沿直线运动,小球做匀加速直线运动,加速度大小 ![]()
由运动学公式得 ![]()
根据牛顿第二定律,有 ![]()
解得 ![]()

练习册系列答案
相关题目