题目内容
14.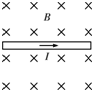 如图所示,一根长为L=0.2m的直导线放在水平方向的匀强磁场中,导线水平且与磁场方向垂直,导线中通有向右的电流.
如图所示,一根长为L=0.2m的直导线放在水平方向的匀强磁场中,导线水平且与磁场方向垂直,导线中通有向右的电流.(1)请判断导线所受安培力的方向是竖直向上还是竖直向下;
(2)若匀强磁场的磁感应强度大小B=0.5T,导线中电流I=1.5A,试计算导线所受安培力的大小.
分析 根据左手定则判断出安培力的方向,当磁场方向与电流方向垂直时,安培力F=BIL,结合公式求出安培力的大小.
解答 解:(1)由左手定则判断安培力的方向竖直向上;
(2)根据安培力公式可得:F=BIL=0.5×1.5×0.2=0.15N;
答:(1)安培力方向竖直向上;
(2)导线所受安培力的大小0.15N.
点评 解决本题的关键知道电流方向与磁场方向平行时,安培力F=0,电流方向与磁场方向垂直时,安培力F=BIL.

练习册系列答案
相关题目
4.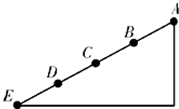 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀速直线运动,下列结论正确的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀速直线运动,下列结论正确的是( )
 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀速直线运动,下列结论正确的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀速直线运动,下列结论正确的是( )| A. | $\frac{{x}_{AB}}{{{t}_{AB}}^{2}}$=$\frac{{x}_{AC}}{{{t}_{AC}}^{2}}$=$\frac{{x}_{AD}}{{{t}_{AD}}^{2}}$=$\frac{{x}_{AE}}{{{t}_{AE}}^{2}}$ | |
| B. | $\frac{{x}_{AB}}{{{t}_{AB}}^{2}}$=$\frac{{x}_{BC}}{{{t}_{BC}}^{2}}$=$\frac{{x}_{CD}}{{{t}_{CD}}^{2}}$=$\frac{{x}_{DE}}{{{t}_{DE}}^{2}}$ | |
| C. | tAB:tAC:tAD:tAE=1:$\sqrt{2}$:$\sqrt{3}$:$\sqrt{4}$ | |
| D. | $\overline{{v}_{AB}}$:$\overline{{v}_{BC}}$:$\overline{{v}_{CD}}$:$\overline{{v}_{DE}}$=1:($\sqrt{2}$+1):($\sqrt{3}$+$\sqrt{2}$):($\sqrt{4}$+$\sqrt{3}$) |
5.关于功和能的联系和区别,下列说法中不正确的是( )
| A. | 功就是能,能就是功 | |
| B. | 功是过程量,能是状态量 | |
| C. | 功是能量转化的量度 | |
| D. | 做功的过程总对应着能量的转化过程 |
9.关于重力以下说法正确的是( )
| A. | 重力的方向总是竖直向下的 | |
| B. | 重力是物体的固有属性,不随位置而改变 | |
| C. | 形状规则的物体的重心,不一定在它的几何中心上 | |
| D. | 挂在绳上静止的物体,它受到的重力就是绳对它的拉力 |
3.如图所示,推力F作用在木块上,木块处于静止状态,则木块的受力个数可能为( )
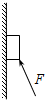

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
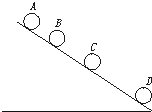 从斜面上某位置,每隔0.1s释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得xAB=15cm,xCD=25cm,试求
从斜面上某位置,每隔0.1s释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得xAB=15cm,xCD=25cm,试求
 如图所示是研究物体做匀变速直线运动规律时得到的一条纸带(实验中打点计时器所接低压交流电源的频率为50Hz),从O点后开始每5个计时点取一个记数点,依照打点的先后顺序依次编号为0、1、2、3、4、5、6,测得S1=5.18cm,S2=4.40cm,S3=3.60cm,S4=2.78cm,S5=2.00cm,S6=1.20cm.(结果保留两位有效数字)
如图所示是研究物体做匀变速直线运动规律时得到的一条纸带(实验中打点计时器所接低压交流电源的频率为50Hz),从O点后开始每5个计时点取一个记数点,依照打点的先后顺序依次编号为0、1、2、3、4、5、6,测得S1=5.18cm,S2=4.40cm,S3=3.60cm,S4=2.78cm,S5=2.00cm,S6=1.20cm.(结果保留两位有效数字)