题目内容
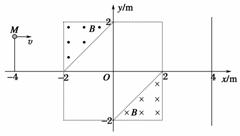
如图14所示,直角坐标系xOy中,x<0的区域存在沿+y轴方向的匀强电场,电场强度大小为E,在x>0的区域存在一垂直纸面的矩形有界匀强磁场,其左边界和下边界分别与Oy、Ox轴重合,磁感应强度大小为B(图中未画出),现有一质量为m,电荷量为e的电子从第二象限的某点P以初速度v0=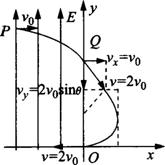
图14
(1)P点的坐标;
(2)矩形区域的最小面积.
(1)设P点的坐标为(x,y),从P到Q电子做类平抛运动,经过Q点时速度与x轴正方向的夹角为θ,cosθ=![]() ,θ=60°.电子在Q点y轴负方向的分速度uy=2v0sinθ.在电场中电子运动的加速度a=
,θ=60°.电子在Q点y轴负方向的分速度uy=2v0sinθ.在电场中电子运动的加速度a=![]() .电子由P点到Q点的时间t,
.电子由P点到Q点的时间t,
vy=at,xP=-v0t,yP=L+![]() at2,
at2,
解得:xP=![]() .yP=
.yP=![]()
(2)设所加最小矩形磁场区域长宽分别为L1、L2,在磁场中做圆周运动半径为r,则
r=![]() 或者(L-r)sin(90°-θ)=r=
或者(L-r)sin(90°-θ)=r=![]()
L1=r+rcosθ,L2=r,S=L![]() (1+cos0),Smin=
(1+cos0),Smin=![]() .
.

练习册系列答案
相关题目
下面是在测某电池的电动势和内电阻的实验中记录的6组数据.请在直角坐标系中画出U-I图,并根据图象算出待测电池的电动势和内电阻.
U/V | 1.37 | 1.32 | 1.24 | 1.18 | 1.10 | 1.05 |
I/A | 0.12 | 0.20 | 0.31 | 0.32 | 0.50 | 0.57 |
解析:建立坐标系,利用描点法画出U-I图象如图

图
直线与纵轴的交点坐标即为电源的电动势E=1.48 V.
从图线上取两点,由其坐标值求直线斜率,则r=![]() =0.76 Ω.
=0.76 Ω.