题目内容
5.关于匀速圆周运动的物理量之间的关系,下列说法正确的是( )| A. | 线速度与半径成正比 | B. | 角速度与半径成反比 | ||
| C. | 周期与角速度成反比 | D. | 加速度与半径成正比 |
分析 根据线速度与半径的关系、角速度与半径的关系分析线速度和角速度,结合周期与角速度的关系式分析周期和角速度的关系.
解答 解:A、根据v=rω知,在角速度一定时,线速度与半径成正比,在线速度一定时,角速度与半径成反比,故A、B错误.
C、根据T=$\frac{2π}{ω}$知,周期与角速度成反比,故C正确.
D、根据a=rω2知,在角速度一定时,加速度与半径成正比,故D错误.
故选:C.
点评 解决本题的关键知道判断三个物理量之间的关系时,只有确定某一个物理量不变,才能确定另外两个物理量之间的关系,基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.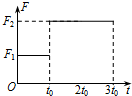 训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )
训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )
 训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )
训练有素的杂技演员在进行“顶杆”表演时,用的是一根长直竹竿(假设竹竿质量不计),演员自杆顶由静止开始下滑,滑到杆底时速度正好为零.已知竹竿底部与下面顶杆人肩部之间有一压力传感器,传感器显示人的肩部受到竹竿底部施加的压力随时间变化情况如图所示,重力加速度为g.则( )| A. | 从竹竿上滑下的演员的质量为$\frac{{F}_{1}+{F}_{2}}{2g}$ | |
| B. | 演员下滑过程中的加速度最大值为$\frac{{F}_{2}-{F}_{1}}{2{F}_{2}+{F}_{1}}$g | |
| C. | 演员下滑的速度最大值为$\frac{{F}_{2}-{F}_{1}}{2{F}_{2}+{F}_{1}}$gt0 | |
| D. | 竹竿的长度为$\frac{3({F}_{2}-{F}_{1})}{2{F}_{2}+{F}_{1}}$gt02 |
16.关于做曲线运动的物体的速度和加速度的以下说法中,正确的是( )
| A. | 速度的方向与大小一定都在时刻变化 | |
| B. | 速度的方向不断发生变化,速度的大小不一定发生变化 | |
| C. | 因为速度的方向不断改变,所以加速度的方向不断改变 | |
| D. | 因为速度的方向不断改变,所以加速度一定不为零,其方向与速度方向不共线 |
20. 如图所示,在倾角为α的光滑斜面上放一个重为G的光滑球,并用光滑的档板挡住与斜面夹角为θ(最初θ<α),挡板可以从图示位置以O为轴向左缓慢转至水平位置.在此过程中球始终处于平衡状态,当挡板对球的弹力大小恰好等于球的重力时,θ的大小可以为( )
如图所示,在倾角为α的光滑斜面上放一个重为G的光滑球,并用光滑的档板挡住与斜面夹角为θ(最初θ<α),挡板可以从图示位置以O为轴向左缓慢转至水平位置.在此过程中球始终处于平衡状态,当挡板对球的弹力大小恰好等于球的重力时,θ的大小可以为( )
 如图所示,在倾角为α的光滑斜面上放一个重为G的光滑球,并用光滑的档板挡住与斜面夹角为θ(最初θ<α),挡板可以从图示位置以O为轴向左缓慢转至水平位置.在此过程中球始终处于平衡状态,当挡板对球的弹力大小恰好等于球的重力时,θ的大小可以为( )
如图所示,在倾角为α的光滑斜面上放一个重为G的光滑球,并用光滑的档板挡住与斜面夹角为θ(最初θ<α),挡板可以从图示位置以O为轴向左缓慢转至水平位置.在此过程中球始终处于平衡状态,当挡板对球的弹力大小恰好等于球的重力时,θ的大小可以为( )| A. | α | B. | 2α | C. | π-α | D. | π-2α |
10. 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )| A. | 小球的机械能守恒 | |
| B. | 小球的重力势能一直减少 | |
| C. | 小球的动能先从零开始增大,后又减小到零,在b点时动能最大 | |
| D. | 到c点时小球的机械能最小,弹簧弹性势能最大 |
14. 如图所示,两个同心放置的共面单匝金属环a和b,一条形磁铁穿过圆心且与环面垂直放置.设穿过圆环a的磁通量为Φa,穿过圆环b的磁通量为Φb,已知两圆环的横截面积分别为Sa和Sb,且Sa<Sb,则穿过两圆环的磁通量大小关系为( )
如图所示,两个同心放置的共面单匝金属环a和b,一条形磁铁穿过圆心且与环面垂直放置.设穿过圆环a的磁通量为Φa,穿过圆环b的磁通量为Φb,已知两圆环的横截面积分别为Sa和Sb,且Sa<Sb,则穿过两圆环的磁通量大小关系为( )
 如图所示,两个同心放置的共面单匝金属环a和b,一条形磁铁穿过圆心且与环面垂直放置.设穿过圆环a的磁通量为Φa,穿过圆环b的磁通量为Φb,已知两圆环的横截面积分别为Sa和Sb,且Sa<Sb,则穿过两圆环的磁通量大小关系为( )
如图所示,两个同心放置的共面单匝金属环a和b,一条形磁铁穿过圆心且与环面垂直放置.设穿过圆环a的磁通量为Φa,穿过圆环b的磁通量为Φb,已知两圆环的横截面积分别为Sa和Sb,且Sa<Sb,则穿过两圆环的磁通量大小关系为( )| A. | Φa=Φb | B. | Φa>Φb | C. | Φa<Φb | D. | 无法确定 |
15.关于小乌从弹弓上由静止开始到落到地面(比一定击中目标)的飞行时间,下列说法正确的是( )
| A. | 小鸟的飞行时间由小鸟与地面间的竖直距离决定,大小不唯一 | |
| B. | 小鸟的飞行时间由小鸟飞行的水平距离决定,大小不唯一 | |
| C. | 小鸟的飞行时间由小鸟与地面间的竖直距离决定,大小是唯一的 | |
| D. | 小鸟的飞行时间由小鸟飞行的水平距离决定,大小是唯一的 |
 如图甲所示,在风洞实验室里,一根足够长且固定在竖直平面的均匀细直杆与水平方向成37°角,质量m=2kg的小球穿在细杆上且静止于距细杆底端O较远的某处.开启送风装置,有水平向左的恒定风力F作用于小球上,在t1=2.5s时刻送风停止.小球沿细杆运动的部分v-t同学如图乙所示,已知送风时,小球第直杆仍然有垂直于直杆向下的压力作用,g取10m/s2,sin37°=0.8.求:
如图甲所示,在风洞实验室里,一根足够长且固定在竖直平面的均匀细直杆与水平方向成37°角,质量m=2kg的小球穿在细杆上且静止于距细杆底端O较远的某处.开启送风装置,有水平向左的恒定风力F作用于小球上,在t1=2.5s时刻送风停止.小球沿细杆运动的部分v-t同学如图乙所示,已知送风时,小球第直杆仍然有垂直于直杆向下的压力作用,g取10m/s2,sin37°=0.8.求: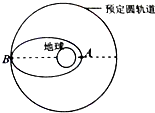 如图所示,是运载火箭发射飞船的示意图,飞船由运载火箭先送人近地点为A、远地点为B的椭圆轨道,在B点实施变轨后,再进入预定圆轨道,已知近地点A距地面高度为h1,飞船在预定圆轨道上飞行n圈所用时间为t,地球表面重力加速度为g,地球半径为R,求:
如图所示,是运载火箭发射飞船的示意图,飞船由运载火箭先送人近地点为A、远地点为B的椭圆轨道,在B点实施变轨后,再进入预定圆轨道,已知近地点A距地面高度为h1,飞船在预定圆轨道上飞行n圈所用时间为t,地球表面重力加速度为g,地球半径为R,求: