题目内容
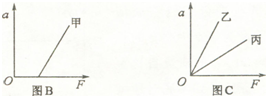 在“探究”加速度与力、质量的关系的实验中,小车及车中砝码的质量用M表示,盘及盘中砝码的质量用m表示,小车的加速度可由小车后拖动的纸 带由打点计时器打出的点计算出.
在“探究”加速度与力、质量的关系的实验中,小车及车中砝码的质量用M表示,盘及盘中砝码的质量用m表示,小车的加速度可由小车后拖动的纸 带由打点计时器打出的点计算出.①当M与m的大小关系满足
②如图B为甲同学根据测量数据作出的a-F图象,说明实验可能存在的问题
③乙、丙同学用同一装置做实验,画出了各自得到的a-F图象如图C所示,两个同学做实验时的哪一个物理量取值不同
④实验中所使用的电源是50Hz的交流电,某同学打好三条纸带,选取其中最好的一条,其中一段如图所示.图中A、B、C、D、E为计数点,相邻两个计数点间有四个点未画出.根据纸带可计算出各计数点的瞬时速度,则VB=

分析:①当盘及盘中砝码的总质量远小于小车及砝码总质量时,可以认为小车受到的拉力等于盘及砝码的重力.
②图线不通过坐标原点,当拉力为某一值时,a为零,知没有平衡摩擦力或倾角过小.
③根据公式F=ma判断a-F图象的斜率.
④匀变速直线运动中,平均速度等于中间时刻的瞬时速度,根据公式△x=aT2求解加速度.
②图线不通过坐标原点,当拉力为某一值时,a为零,知没有平衡摩擦力或倾角过小.
③根据公式F=ma判断a-F图象的斜率.
④匀变速直线运动中,平均速度等于中间时刻的瞬时速度,根据公式△x=aT2求解加速度.
解答:解:①该实验的研究对象是小车,采用控制变量法研究.当质量一定时,研究小车的加速度和小车所受合力的关系.为消除摩擦力对实验的影响,可以把木板D的左端适当垫高,以使小车的重力沿斜面分力和摩擦力抵消,那么小车的合力就是绳子的拉力.
根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
=
?mg
当M>>m时,即当砝码和盘的总重力要远小于小车的重力,绳子的拉力近似等于砝码和盘的总重力.
②从图B中发现直线没过原点,当F≠0时,a=0.也就是说当绳子上有拉力时小车的加速度还为0,说明小车的摩擦力与绳子的拉力抵消呢.该组同学实验操作中遗漏了平衡摩擦力或平衡摩擦力不足这个步骤.即没有平衡摩擦力或平衡摩擦力不够.
③根据牛顿第二定律,a-F图象的斜率表示
,斜率不同,说明小车及车中砝码的总质量M不同.
④B点速度等于AC段的平均速度,为:
vB=
=
=0.877m/s
根据公式△x=aT2,加速度为:
a=
=
=
=3.51m/s2
故答案为:
①M>>m;
②没有平衡摩擦力或平衡摩擦力不够;
③小车及车中砝码的总质量M;
④0.877m/s,3.51m/s2.
根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
| Mmg |
| M+m |
| 1 | ||
1+
|
当M>>m时,即当砝码和盘的总重力要远小于小车的重力,绳子的拉力近似等于砝码和盘的总重力.
②从图B中发现直线没过原点,当F≠0时,a=0.也就是说当绳子上有拉力时小车的加速度还为0,说明小车的摩擦力与绳子的拉力抵消呢.该组同学实验操作中遗漏了平衡摩擦力或平衡摩擦力不足这个步骤.即没有平衡摩擦力或平衡摩擦力不够.
③根据牛顿第二定律,a-F图象的斜率表示
| 1 |
| M |
④B点速度等于AC段的平均速度,为:
vB=
| xAC |
| 2T |
| 0.1754m |
| 2×0.1s |
根据公式△x=aT2,加速度为:
a=
| △x |
| T2 |
| CE-AC |
| T2 |
| (0.491-0.1754)-0.1754 |
| 0.12 |
故答案为:
①M>>m;
②没有平衡摩擦力或平衡摩擦力不够;
③小车及车中砝码的总质量M;
④0.877m/s,3.51m/s2.
点评:解决实验问题通常首先要掌握该实验原理,然后根据实验原理进行数据处理和误差分析;本题中涉及减小系统误差的两条措施:平衡摩擦力,使小车质量远大于砝码质量.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

 在“探究加速度与力的关系”时,保持小车的质量不变,改变小桶中砝码的质量,该同学根据实验数据作出了加速度a与合力F图线如图,该图线不通过坐标原点,试分析图线不通过坐标原点的原因.
在“探究加速度与力的关系”时,保持小车的质量不变,改变小桶中砝码的质量,该同学根据实验数据作出了加速度a与合力F图线如图,该图线不通过坐标原点,试分析图线不通过坐标原点的原因. 在“探究加速度与力、质量的关系”的实验中,当小车质量一定时,根据实验数据画出加速度a与作用力F的图线如图所示.
在“探究加速度与力、质量的关系”的实验中,当小车质量一定时,根据实验数据画出加速度a与作用力F的图线如图所示.