题目内容
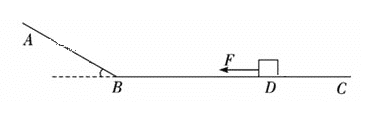
【题目】如图所示一足够长的光滑斜面倾角为37°,斜面AB与水平面BC平滑连接。质量m=1kg可视为质点的物体置于水平面上的D点,D点距B点d=7m,物体与水平面间的动摩擦因数为0.4。现使物体受到一水平向左的恒力F=6.5N作用,经时间t=2s后撤去该力,物体经过B点时的速率不变,重力加速度g取10m/s2,sin37°=0.6,求:
(1)撤去拉力F时物体的位移;
(2)撤去拉力F后,物体经过多长时间第二次经过B点;
(3)物体最后停下的位置距B点多远?
【答案】(1)5m;(2)1.5s;(3)1.125m
【解析】
(1)物体在水平面上运动过程中,设撤去F前后物体的加速度大小分别为a1、a2
由牛顿第二定律得:
![]()
![]()
代入解得:
a1=2.5m/s2
a2=4m/s2
恒力F作用t=2s时物体的位移为:
![]()
故撤去外力F时,物体的位移为5m。
(2)撤去外力瞬间,物体的速度为:
![]()
设撤去拉力F后,物体第一次经过B点的时间为t1
则:
![]()
代入解得:
t1=0.5s
物体滑到B点时速度大小为:
![]()
设物体在斜面上运动的加速度大小为a3
则:
![]()
解得:
![]()
物体在斜面上滑行的总时间:
![]()
所以物体第二次经过B点的时间为:
![]()
(3)物块最后停下的位置距B点:
![]()

练习册系列答案
相关题目