题目内容
(选修模块3-3)
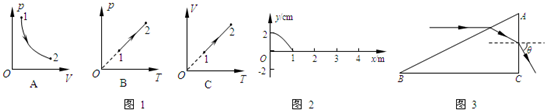
(1)如图1所示,一定质量的理想气体分别在温度T1和T2情形下做等温变化的p-V图象,则下列关于T1和T2大小的说法,正确的是
A.T1大于T2 B.T1小于T2 C.T1等于T2 D.无法比较
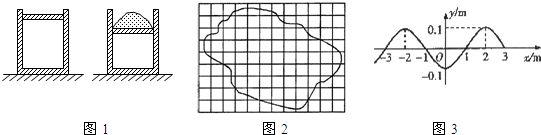
(2)如图2甲所示,将封有一定质量空气的密闭塑料袋从海拔500m、气温为18℃的山脚下带到海拔3200m、气温为10℃的山顶上,情形如图2乙所示.图
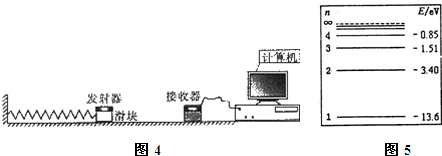
(3)如图3所示,IBM的科学家在铜表面将48个铁原子排成圆圈,形成半径为7.13nm的“原子围栏”,相邻铁原子间有间隙.估算原子平均间隙的大小.结果保留一位有效数字.已知铁的密度7.8×103kg/m3,摩尔质量是5.6×10-2kg/mol,阿伏加德罗常数NA=6.02×1023mol-1.

(1)如图1所示,一定质量的理想气体分别在温度T1和T2情形下做等温变化的p-V图象,则下列关于T1和T2大小的说法,正确的是
A
A
.A.T1大于T2 B.T1小于T2 C.T1等于T2 D.无法比较
(2)如图2甲所示,将封有一定质量空气的密闭塑料袋从海拔500m、气温为18℃的山脚下带到海拔3200m、气温为10℃的山顶上,情形如图2乙所示.图
甲
甲
(选填“甲”或“乙”)中袋中气体分子平均动能大.从甲图到乙图过程中,袋内气体减小的内能大于
大于
(选填“大于”、“等于”或“小于”)气体放出的热量.(3)如图3所示,IBM的科学家在铜表面将48个铁原子排成圆圈,形成半径为7.13nm的“原子围栏”,相邻铁原子间有间隙.估算原子平均间隙的大小.结果保留一位有效数字.已知铁的密度7.8×103kg/m3,摩尔质量是5.6×10-2kg/mol,阿伏加德罗常数NA=6.02×1023mol-1.

分析:(1)根据一定质量的理想气体状态方程
=c(常数)结合图象的含义可正确解答;
(2)温度是分子平均动能的标志,由于气体分子之间的距离很大,因此作用力为零,分子势能为零,所以一定质量气体的内能由其温度决定,根据热力学第一定律可知内能变化与放热之间关系;
(3)根据阿伏伽德罗常数的含义,可以求出一个铁原子的体积,将铁原子看做球形,由此可以求出铁原子直径的大小,根据铁原子所围成圆的周长可以求出原子之间的空隙.
| PV |
| T |
(2)温度是分子平均动能的标志,由于气体分子之间的距离很大,因此作用力为零,分子势能为零,所以一定质量气体的内能由其温度决定,根据热力学第一定律可知内能变化与放热之间关系;
(3)根据阿伏伽德罗常数的含义,可以求出一个铁原子的体积,将铁原子看做球形,由此可以求出铁原子直径的大小,根据铁原子所围成圆的周长可以求出原子之间的空隙.
解答:解:(1)根据一定质量的理想气体状态方程可知:
=c(常数),由此可知T1>T2,故A正确,BCD错误.
故选A.
(2)将封有一定质量空气的密闭塑料袋从山底移动到山顶时,根据
=c(常数)可知其体积增大,因此乙图中塑料袋是处于山顶的,温度是分子平均动能的标志,由于山顶温度低,因此分子平均动能小,山底的塑料袋中分子平均动能高于山顶的,即甲中气体分子平均动能大;从甲到乙过程中,温度降低,内能减小,体积增大,气体对外做功,由△U=E+Q可知,气体内能内能减小大于气体放出的热量.
故答案为:甲;大于.
(3)根据题意有:
一个铁原子的体积:V=
将铁原子看做球形,因此铁原子的直径为:D=
围栏中相邻铁原子的平均间隙:l=
-D
解得:l=7×10-10m.
故原子平均间隙的大小:l=7×10-10m.
| PV |
| T |
故选A.
(2)将封有一定质量空气的密闭塑料袋从山底移动到山顶时,根据
| PV |
| T |
故答案为:甲;大于.
(3)根据题意有:
一个铁原子的体积:V=
| M |
| ρNA |
将铁原子看做球形,因此铁原子的直径为:D=
|
围栏中相邻铁原子的平均间隙:l=
| 2πr |
| n |
解得:l=7×10-10m.
故原子平均间隙的大小:l=7×10-10m.
点评:有关气体状态方程和热力学第一定律相结合的问题是考查的重点,要加强这方面的练习;同时要加强有关阿伏伽德罗常数的运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
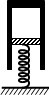 ,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
,弹簧一端固定于水平面上,另一端与质量为m的活塞拴接在一起,开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体.气缸和活塞均可与外界进行热交换.若外界环境的温度缓慢降低,则封闭气体的体积将
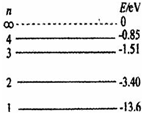
 C.(选修模块 3 一 5 )
C.(选修模块 3 一 5 )