题目内容
用平行于斜面的力推动一个质量为m的物体沿着倾角为θ的光滑斜面向上运动当物体运动到斜面中点时撤去外推力,物体恰能滑到斜面项点.由此可以断定推力F的大小必定为
- A.2mgcosθ
- B.2mgsinθ
- C.mg(1-sinθ)
- D.2mg(1+sinθ)
B
分析:根据牛顿第二定律求出匀加速上滑和匀减速上滑的加速度大小,抓住位移相等,得出加速度的关系,从而求出推力F的大小.
解答:根据题意知,匀加速直线运动和匀减速直线运动的位移相等,根据x=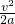 知,匀加速直线运动和匀减速直线运动的加速度相等.
知,匀加速直线运动和匀减速直线运动的加速度相等.
匀加速直线运动的加速度 ,匀减速直线运动的加速度大小
,匀减速直线运动的加速度大小 .
.
a1=a2
解得F=2mgsinθ.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键通过匀加速和匀减速直线运动的位移相等,得出加速度的关系,从而根据牛顿第二定律进行求解.
分析:根据牛顿第二定律求出匀加速上滑和匀减速上滑的加速度大小,抓住位移相等,得出加速度的关系,从而求出推力F的大小.
解答:根据题意知,匀加速直线运动和匀减速直线运动的位移相等,根据x=
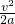 知,匀加速直线运动和匀减速直线运动的加速度相等.
知,匀加速直线运动和匀减速直线运动的加速度相等.匀加速直线运动的加速度
 ,匀减速直线运动的加速度大小
,匀减速直线运动的加速度大小 .
.a1=a2
解得F=2mgsinθ.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键通过匀加速和匀减速直线运动的位移相等,得出加速度的关系,从而根据牛顿第二定律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目