题目内容
【题目】用一根长1m的轻质细绳将一幅质量为1kg的画框对称悬挂在墙壁上，已知绳能承受的最大张力10N，为使绳不断裂，画框上两个钉的间距最大为（g取10m/s2）（ ）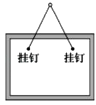
A.
m
B.
m
C.
D.
m
【答案】B
【解析】解：一个大小方向确定的力分解为两个等大的力时，合力在分力的角平分线上，且两分力的夹角越大，分力越大，因而当绳子拉力达到F=10N的时候，绳子间的张角最大，为120°，此时两个挂钉间的距离最大；
画框受到重力和绳子的拉力，三个力为共点力，受力如图．
绳子与竖直方向的夹角为θ=60°，绳子长为L0=1m，
则有mg=2Fcosθ，两个挂钉的间距离L=2 
sinθ，
解得L= 
m；
所以答案是：B
【考点精析】掌握力的合成是解答本题的根本，需要知道求几个已知力的合力，叫做力的合成；共点的两个力（F 1 和F 2 ）合力大小F的取值范围为:|F 1 -F 2 |≤F≤F 1 +F 2．
练习册系列答案
同步拓展阅读系列答案
相关题目
