题目内容
16.一个木块静止在光滑水平面上,一颗子弹水平射入木块未穿出,当子弹刚好相对木块静止时,木块发生位移为s,设子弹受到木块的阻力大小恒定,子弹射入木块中的深度为d,则s与d的关系为s小于d(填大于,等于或小于)分析 由动量守恒的条件可知系统总动量守恒;分别对M、m由动能定理可得出s与d的关系.
解答 解:令子弹质量为m,速度为v0,木块质量为M,速度为设子弹射入木块后二者的共同速度为v,子弹击中木块过程系统动力守恒,以子弹的初速度方向为正方向,由动量守恒定律得:
mv0=(M+m)v ,
,
设子弹与木块之间的相互作用力为f,由动能定理得:
对子弹:-f (s+d)=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$,
对木块:fs=$\frac{1}{2}M{v}^{2}$
解得:$\frac{s}{d}=\frac{m}{M+m}$
因为$\frac{m}{m+M}<1$<1,所以s<d;
故答案为:小于.
点评 本题为动量定恒与动能定理的结合题目,注意在解题中应灵活选取研究对象,应用动量定恒或动能定理列式求解.

练习册系列答案
相关题目
6. 如图所示,在正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带正电的粒子(不计重力)从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )
如图所示,在正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带正电的粒子(不计重力)从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )
 如图所示,在正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带正电的粒子(不计重力)从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )
如图所示,在正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带正电的粒子(不计重力)从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )| A. | 粒子的运动轨迹一定经过P点 | |
| B. | 粒子的运动轨迹一定经过PE之间某点 | |
| C. | 若将粒子的初速度变为原来的一半,粒子恰好由E点射出正方形ABCD区域 | |
| D. | 若将粒子的初速度变为原来的2倍,粒子会由DH的中点射出正方形ABCD区域 |
11.下列说法正确的是( )
| A. | 运动得越快的汽车越不容易停下来,是因为汽车运动得越快,惯性越大 | |
| B. | 不管物体匀速运动时,还是变速运动时,都存在惯性 | |
| C. | 只有静止的物体受到的摩擦力才叫静摩擦力 | |
| D. | 滑动摩擦力不可能是物体运动的动力 |
1.(多选)小明骑自行车由静止沿直线运动,他在第1s内、第2s内、第3s内、第4s内通过的位移分别为1m、2m、3m、4m,则( )
| A. | 他在第4s末的瞬时速度为4m/s | B. | 他在第2s内的平均速度为2m/s | ||
| C. | 他在4s内的平均速度为2.5m/s | D. | 他在1s末的瞬时速度为1m/s |
1. 如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是( )
如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是( )
 如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是( )
如图,质量为M、长度为L的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为f.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是( )| A. | 物块到达小车最右端时具有的动能为F (L+s) | |
| B. | 物块到达小车最右端时,小车具有的动能为f s | |
| C. | 物块克服摩擦力所做的功为f (L+s) | |
| D. | 物块和小车增加的机械能为f s |

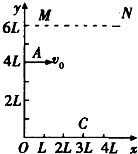 如图,在xOy平面内,MN和x轴之间有平行于y轴的匀强电场和垂直于xOy平面的匀强磁场,y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动.如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.不计重力的影响,求:
如图,在xOy平面内,MN和x轴之间有平行于y轴的匀强电场和垂直于xOy平面的匀强磁场,y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动.如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.不计重力的影响,求:
 如图所示,空气中一块圆截异型玻璃砖,折射率为$\sqrt{2}$,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.求入射点P距圆心O的距离.
如图所示,空气中一块圆截异型玻璃砖,折射率为$\sqrt{2}$,现有一束细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行返回,角AOB为135°,圆半径为r.求入射点P距圆心O的距离.