题目内容
质量为1.0kg的物体静止在水平面上,物体与水平面之间的动摩擦因数为0.20. 对物体施加一个大小变化、方向不变的水平拉力F,使物体在水平面上运动了3t0的时间.为使物体在3t0时间内发生的位移最大,力F随时间变化情况应该为下面四个图中的哪一个
- A.

- B.
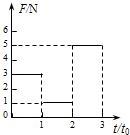
- C.
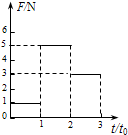
- D.
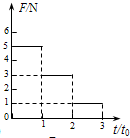
D
分析:根据牛顿第二定律求出加速度,由位移公式求出各段时间内物体的位移,再确定哪种情况位移最大.
解答:
A、在0-1s内,F<μmg,物体静止不动.在1-2s内,加速度a1=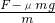 =1m/s2,位移x1=
=1m/s2,位移x1=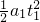 =0.5m,第2s末速度为v=a1t1=0.5m/s.在2-3s内,加速度a2=
=0.5m,第2s末速度为v=a1t1=0.5m/s.在2-3s内,加速度a2=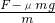 =3m/s2,位移为x2=vt2
=3m/s2,位移为x2=vt2 =2m.
=2m.
C、在0-1s内,F<μmg,物体静止不动.在1-2s内,加速度a1=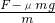 =3m/s2,位移x1=
=3m/s2,位移x1=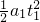 =1.5m,第2s末速度为v=a1t1=1.5m/s.在2-3s内,加速度a2=
=1.5m,第2s末速度为v=a1t1=1.5m/s.在2-3s内,加速度a2=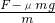 =1m/s2,位移为x2=vt2
=1m/s2,位移为x2=vt2 =2m.
=2m.
B、在0-1s内,加速度a1=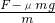 =3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=
=3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=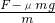 =-0.5m/s2,位移x2=v1t2+
=-0.5m/s2,位移x2=v1t2+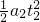 =2.75m,第2s末速度为v2=v1+a2t2=2.5m/s.在2-3s内,加速度a3=
=2.75m,第2s末速度为v2=v1+a2t2=2.5m/s.在2-3s内,加速度a3=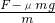 =1m/s2,位移为x3=v2t3+
=1m/s2,位移为x3=v2t3+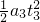 =3m.
=3m.
D、在0-1s内,加速度a1=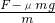 =3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=
=3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=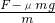 =1m/s2,位移x2=v1t2+
=1m/s2,位移x2=v1t2+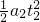 =3.5m,第2s末速度为v2=v1+a2t2=3.5m/s.在2-3s内,加速度a2=
=3.5m,第2s末速度为v2=v1+a2t2=3.5m/s.在2-3s内,加速度a2=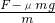 =-0.5m/s2,位移为x3=v2t3
=-0.5m/s2,位移为x3=v2t3 =3.25m.
=3.25m.
故选D
点评:本题也可以通过计算加速度和速度,作出速度-时间图象,根据“面积”表示位移,判断位移的大小.
分析:根据牛顿第二定律求出加速度,由位移公式求出各段时间内物体的位移,再确定哪种情况位移最大.
解答:
A、在0-1s内,F<μmg,物体静止不动.在1-2s内,加速度a1=
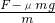 =1m/s2,位移x1=
=1m/s2,位移x1=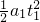 =0.5m,第2s末速度为v=a1t1=0.5m/s.在2-3s内,加速度a2=
=0.5m,第2s末速度为v=a1t1=0.5m/s.在2-3s内,加速度a2=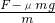 =3m/s2,位移为x2=vt2
=3m/s2,位移为x2=vt2 =2m.
=2m.C、在0-1s内,F<μmg,物体静止不动.在1-2s内,加速度a1=
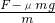 =3m/s2,位移x1=
=3m/s2,位移x1=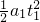 =1.5m,第2s末速度为v=a1t1=1.5m/s.在2-3s内,加速度a2=
=1.5m,第2s末速度为v=a1t1=1.5m/s.在2-3s内,加速度a2=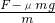 =1m/s2,位移为x2=vt2
=1m/s2,位移为x2=vt2 =2m.
=2m.B、在0-1s内,加速度a1=
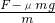 =3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=
=3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=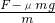 =-0.5m/s2,位移x2=v1t2+
=-0.5m/s2,位移x2=v1t2+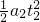 =2.75m,第2s末速度为v2=v1+a2t2=2.5m/s.在2-3s内,加速度a3=
=2.75m,第2s末速度为v2=v1+a2t2=2.5m/s.在2-3s内,加速度a3=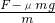 =1m/s2,位移为x3=v2t3+
=1m/s2,位移为x3=v2t3+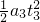 =3m.
=3m.D、在0-1s内,加速度a1=
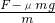 =3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=
=3m/s2,第1s末速度为v1=a1t1=3m/s.在1-2s内,加速度a2=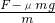 =1m/s2,位移x2=v1t2+
=1m/s2,位移x2=v1t2+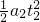 =3.5m,第2s末速度为v2=v1+a2t2=3.5m/s.在2-3s内,加速度a2=
=3.5m,第2s末速度为v2=v1+a2t2=3.5m/s.在2-3s内,加速度a2=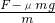 =-0.5m/s2,位移为x3=v2t3
=-0.5m/s2,位移为x3=v2t3 =3.25m.
=3.25m.故选D
点评:本题也可以通过计算加速度和速度,作出速度-时间图象,根据“面积”表示位移,判断位移的大小.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
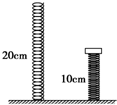 如图所示,一轻质弹簧竖直放置在水平地面上,下端固定.弹簧原长为20cm,劲度系数k=200N/m.现用竖直向下的力将弹簧压缩到10cm后用细线栓住,此时在弹簧上端放置质量为1.0kg的物块.在烧断细线的瞬间( )
如图所示,一轻质弹簧竖直放置在水平地面上,下端固定.弹簧原长为20cm,劲度系数k=200N/m.现用竖直向下的力将弹簧压缩到10cm后用细线栓住,此时在弹簧上端放置质量为1.0kg的物块.在烧断细线的瞬间( )| A、物块的速度为零、加速度也为零 | B、物块的加速度为10.0m/s2,方向竖直向上、速度为零 | C、物块的加速度为零,但速度不为零 | D、物块的加速度为30.0m/s2,方向竖直向下 |
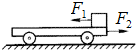 如图所示,质量2.0kg的小车放在光滑水平面上,在小车右端放一质量为1.0kg的物块,物块与小车之间的动摩擦因数为0.5,当物块与小车同时分别受到水平向左F1=6.0N的拉力和水平向右F2=9.0N的拉力,经0.4s同时撤去两力.(g取10m/s2)
如图所示,质量2.0kg的小车放在光滑水平面上,在小车右端放一质量为1.0kg的物块,物块与小车之间的动摩擦因数为0.5,当物块与小车同时分别受到水平向左F1=6.0N的拉力和水平向右F2=9.0N的拉力,经0.4s同时撤去两力.(g取10m/s2) 已知一些材料间的动摩擦因数如下表所示:
已知一些材料间的动摩擦因数如下表所示: