题目内容
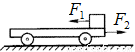
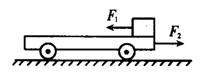
 如图所示,质量2.0kg的小车放在光滑水平面上,在小车右端放一质量为1.0kg的物块,物块与小车之间的动摩擦因数为0.5,当物块与小车同时分别受到水平向左F1=6.0N的拉力和水平向右F2=9.0N的拉力,经0.4s同时撤去两力.(g取10m/s2)
如图所示,质量2.0kg的小车放在光滑水平面上,在小车右端放一质量为1.0kg的物块,物块与小车之间的动摩擦因数为0.5,当物块与小车同时分别受到水平向左F1=6.0N的拉力和水平向右F2=9.0N的拉力,经0.4s同时撤去两力.(g取10m/s2)试求:(1)撤去两力时,物块与小车的速度分别为多少?
(2)为使物块不从小车上滑下,求小车最少要多长?
分析:(1)对小车和物块进行受力分析,根据牛顿第二定律求出加速度,根据速度时间关系即可求解速度;
(2)根据能量守恒定律求出小车的长度.
(2)根据能量守恒定律求出小车的长度.
解答:解:(1)对物块进行受力分析,根据牛顿第二定律得:
a1=
=
=1m/s2
所以物体的速度:v1=a1t=0.4m/s
对小车进行受力分析,根据牛顿第二定律得:
a2=
=
=2m/s2
所以小车的速度:v2=a2t=0.8m/s
(2)撤去外力之前,物块的位移x1=
a1t2=0.08m
小车运动的位移为:x2=
a2t2=0.16m
撤去外力后,两者速度相等后就不会滑下,根据动量守恒定律得:
Mv2-mv1=(m+M)v
解得:v=0.4m/s
系统的动能减小转化为内能,当物块运动到小车左端时,两者速度刚好相等.根据能量守恒定律得:
μmgs=
mv12+
Mv22-
(m+M)v 2
代入解得,s=0.096m
所以小车的最小长度为L=x1+x2+s=0.336m
答:
(1)撤去两力时,物块的速度为0.4m/s,小车的速度为0.8m/s;
(2)小车至少0.336m,物块才不会从小车上掉下去.
a1=
| F1-μmg |
| m |
| 6-0.5×1×10 |
| 1 |
所以物体的速度:v1=a1t=0.4m/s
对小车进行受力分析,根据牛顿第二定律得:
a2=
| F2-μmg |
| M |
| 9-0.5×1×10 |
| 2 |
所以小车的速度:v2=a2t=0.8m/s
(2)撤去外力之前,物块的位移x1=
| 1 |
| 2 |
小车运动的位移为:x2=
| 1 |
| 2 |
撤去外力后,两者速度相等后就不会滑下,根据动量守恒定律得:
Mv2-mv1=(m+M)v
解得:v=0.4m/s
系统的动能减小转化为内能,当物块运动到小车左端时,两者速度刚好相等.根据能量守恒定律得:
μmgs=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入解得,s=0.096m
所以小车的最小长度为L=x1+x2+s=0.336m
答:
(1)撤去两力时,物块的速度为0.4m/s,小车的速度为0.8m/s;
(2)小车至少0.336m,物块才不会从小车上掉下去.
点评:有时运用动量守恒定律研究物体的速度,比牛顿第二定律和运动学公式结合简单,因为动量守恒定律不涉及运动的细节和过程.

练习册系列答案
相关题目
 .5,当物块与小车同时分别受到水平向左
.5,当物块与小车同时分别受到水平向左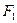 =6.0N的拉力和水平向右
=6.0N的拉力和水平向右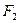 =9.0N的拉力,经0.4s同时撤去两力.(g取10
=9.0N的拉力,经0.4s同时撤去两力.(g取10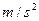 )
)
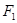 =6.0N的拉力和水平向右
=6.0N的拉力和水平向右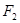 =9.0N的拉力,经0.4s同时撤去两力.(g取10
=9.0N的拉力,经0.4s同时撤去两力.(g取10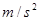 )
)