题目内容
3.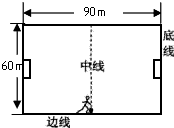 足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中.某足球场长90m、宽60m.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为l2m/s的匀减速直线运动,加速度大小为2m/s2.试求:
足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中.某足球场长90m、宽60m.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为l2m/s的匀减速直线运动,加速度大小为2m/s2.试求:(1)足球从开始做匀减速运动到停下来的位移为多大?
(2)足球开始做匀减速直线运动的同时,该前锋队员沿边线向前追赶足球.他的启动过程可以视为初速度为0,加速度为2m/s2的匀加速直线运动,他能达到的最大速度为8m/s.该前锋队员至少经过多长时间能追上足球?
(3)若该前锋队员追上足球后,又将足球以速度v沿边线向前踢出,足球的运动仍视为加速度大小为2m/s2的匀减速直线运动.与此同时,由于体力的原因,该前锋队员以6m/s的速度做匀速直线运动向前追赶足球,若该前锋队员恰能在底线追上足球,求速度v的大小?
分析 (1)根据速度时间公式求出足球匀减速直线运动的时间,从而根据平均速度公式求出足球的位移.
(2)根据速度时间公式求出运动员达到最大速度的时间和位移,然后运动员做匀速直线运动,结合位移关系求出追及的时间.
(3)结合运动员和足球的位移关系,运用运动学公式求出前锋队员在底线追上足球时的速度.
解答 解:(1)足球匀减速运动的时间为${t}_{1}=\frac{{v}_{1}}{{a}_{1}}=\frac{12}{2}s=6s$,运动位移为${x}_{1}=\frac{{v}_{1}}{2}{t}_{1}=\frac{12}{2}×6m=36m$.
(2)前锋队员做匀加速运动达到最大速度的时间和位移分别为:${t}_{2}=\frac{{v}_{2}}{{a}_{2}}=\frac{8}{2}s=4s$,则 ${x}_{2}=\frac{{v}_{2}}{2}{t}_{2}=\frac{8}{2}×4m=16m$.
之后前锋队员做匀速直线运动,到足球停止运动时,其位移为:x3=v2(t1-t2)=8×(6-4)m=16m
由于x2+x3<x1,故足球停止运动时,前锋队员没有追上足球,然后前锋队员继续以最大速度匀速运动追赶足球,
由匀速运动公式得x1-(x2+x3)=v2t3,
代入数据得:t3=0.5s
前锋队员追上足球的时间t=t1+t3=6.5s
(3)此时足球距底线的距离为:x4=45-x1=45-36m=9m
设前锋队员运动到底线的时间为t4,则有x4=v3t4
足球在t4时间内发生的位移为${x_4}=v{t_4}-\frac{1}{2}{a_1}t_4^2$
联立以上各式代入数据解得:v=7.5m/s.
答:(1)足球从开始做匀减速运动到停下来的位移为36m.
(2)前锋队员至少经过6.5s能追上足球.
(3)若该前锋队员恰能在底线追上足球,速度为7.5m/s.
点评 解决本题的关键理清足球和运动员的位移关系,结合运动学公式灵活求解.由于是多过程问题,解答时需细心.

 每课必练系列答案
每课必练系列答案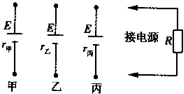 如图所示,用甲、乙、丙三个电动势E相同而内电阻r不同的电源,分别给定值电阻R供电.已知甲、乙、丙三个电源内阻的大小关系为r甲>r乙>r丙,则将R先后接在这三个电源上时的情况相比,下列说法中正确的是( )
如图所示,用甲、乙、丙三个电动势E相同而内电阻r不同的电源,分别给定值电阻R供电.已知甲、乙、丙三个电源内阻的大小关系为r甲>r乙>r丙,则将R先后接在这三个电源上时的情况相比,下列说法中正确的是( )| A. | 接在甲电源上时,通过R的电流最大 | |
| B. | 接在丙电源上时,通过R的电流最大 | |
| C. | 接在乙电源上时,电阻R消耗的电功率最大 | |
| D. | 接在丙电源上时,电阻R消耗的电功率最大 |
| A. | 28J | B. | 64J | C. | 32J | D. | 36J |
 如图所示,表面粗糙的固定斜面顶端安有滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态.当用水平向左的恒力F推Q时,P、Q仍静止不动,则( )
如图所示,表面粗糙的固定斜面顶端安有滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态.当用水平向左的恒力F推Q时,P、Q仍静止不动,则( )| A. | Q受到的摩擦力一定变小 | B. | Q受到的摩擦力变化情况不能确定 | ||
| C. | 轻绳上的拉力一定变小 | D. | 轻绳上拉力一定不变 |
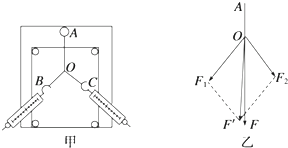
 (1)在做“探究力的合成方法”实验时,橡皮条的一端固定在木板上,用两个弹簧测力计把橡皮条的另一端拉到某一确定的O点,以下操作中错误的是ACD.
(1)在做“探究力的合成方法”实验时,橡皮条的一端固定在木板上,用两个弹簧测力计把橡皮条的另一端拉到某一确定的O点,以下操作中错误的是ACD.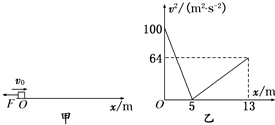 如图甲所示,物块的质量m=1kg,初速度v0=10m/s,在一水平向左的恒力F作用下从O点沿粗糙的水平面向右运动,某时刻后恒力F突然反向,大小不变,整个过程中物块速度的平方随位置坐标变化的关系图象如图乙所示,g=10m/s2.
如图甲所示,物块的质量m=1kg,初速度v0=10m/s,在一水平向左的恒力F作用下从O点沿粗糙的水平面向右运动,某时刻后恒力F突然反向,大小不变,整个过程中物块速度的平方随位置坐标变化的关系图象如图乙所示,g=10m/s2. 出租车上安装有速度表,计价器里安装有里程表和时间表.出租车载客后,从10时10分55秒由静止开始做匀加速直线运动,到10时11分05秒时,速度表显示36km/h.求:
出租车上安装有速度表,计价器里安装有里程表和时间表.出租车载客后,从10时10分55秒由静止开始做匀加速直线运动,到10时11分05秒时,速度表显示36km/h.求: