题目内容
2.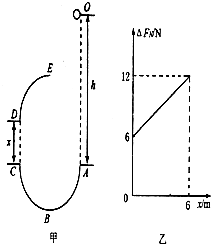 如图甲,半圆弧ABC与四分之一圆弧DE是同一竖直平面内的两个半径相同的光滑轨道,其最高点E与最低点B各安装了一个压力传感器;CD连线与两轨道相切且竖直,间距为x.若在A点正上方的O点将一小球由静止释放,小球下落h后从A点切入轨道并从E点离开轨道.现改变CD间的距离,测得小球通过B、E两点的压力差△FN与距离x的关系如图乙所示,不计空气阻力,取g=10m/s2,求:光滑轨道的半径R.
如图甲,半圆弧ABC与四分之一圆弧DE是同一竖直平面内的两个半径相同的光滑轨道,其最高点E与最低点B各安装了一个压力传感器;CD连线与两轨道相切且竖直,间距为x.若在A点正上方的O点将一小球由静止释放,小球下落h后从A点切入轨道并从E点离开轨道.现改变CD间的距离,测得小球通过B、E两点的压力差△FN与距离x的关系如图乙所示,不计空气阻力,取g=10m/s2,求:光滑轨道的半径R.
分析 应用动能定理求出B、E两点的速度关系,由牛顿第二定律求出小球在B、E点对轨道的压力差,然后根据图示图象求出轨道半径.
解答 解:从B到E过程,由动能定理得:-mg(2R+x)=$\frac{1}{2}$mvE2-$\frac{1}{2}$mvB2,
小球在圆弧轨道做圆周运动,由牛顿第二定律得:
在B点:FB-mg=m$\frac{{v}_{B}^{2}}{R}$,
在E点:FE+mg=m$\frac{{v}_{E}^{2}}{R}$,
在两点的压力差:△FN=FB′-FE′=FB-FE,
解得:△FN=6mg+$\frac{2mg}{R}$x,
由图示:△FN-x图象可知,
截距:b=6mg=6,解得:m=0.1kg,
斜率:k=$\frac{2mg}{R}$=$\frac{12-6}{6}$=1,轨道半径:R=2mg=2m;
答:光滑轨道的半径R为2m.
点评 本题是一道力学综合题,分析清楚小球的运动过程、求出图象的函数表达式是解题的关键,应用动能定理与牛顿第二定律可以解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图所示,静止的传送带上有一木块A正在匀速下滑,当传送带突然向下开动时,木块滑到底部所需的时间t与传送带静止不动时所需时间t0相比( )
如图所示,静止的传送带上有一木块A正在匀速下滑,当传送带突然向下开动时,木块滑到底部所需的时间t与传送带静止不动时所需时间t0相比( )
 如图所示,静止的传送带上有一木块A正在匀速下滑,当传送带突然向下开动时,木块滑到底部所需的时间t与传送带静止不动时所需时间t0相比( )
如图所示,静止的传送带上有一木块A正在匀速下滑,当传送带突然向下开动时,木块滑到底部所需的时间t与传送带静止不动时所需时间t0相比( )| A. | 一定是t=t0 | B. | 一定是t>t0 | C. | 一定是t<t0 | D. | 可能是t=t0 |
13.物体自O点由静止开始做匀加速直线运动,途径A、B、C三点,其中A、B之间的距离L1=3m,B、C之间的距离L2=4m.若物体通过L1、L2这两段位移的时间相等,则O、A之间的距离L等于( )
| A. | 0.75m | B. | 1m | C. | $\frac{25}{8}$m | D. | $\frac{9}{8}$m |
10. 新修订的《国家学生体质健康标准》将“引体向上”作为男同学的必测项目.如图所示.质量为50kg的某同学两手正提单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下顎距单杠面的高度为0.6m.然后用恒力向上拉,经过1s下颚到达单杠.不考虑空气阻力和因手臀穹曲而引起人的重心相对人体位置的变化,取g=1Om/s2.则该同学( )
新修订的《国家学生体质健康标准》将“引体向上”作为男同学的必测项目.如图所示.质量为50kg的某同学两手正提单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下顎距单杠面的高度为0.6m.然后用恒力向上拉,经过1s下颚到达单杠.不考虑空气阻力和因手臀穹曲而引起人的重心相对人体位置的变化,取g=1Om/s2.则该同学( )
 新修订的《国家学生体质健康标准》将“引体向上”作为男同学的必测项目.如图所示.质量为50kg的某同学两手正提单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下顎距单杠面的高度为0.6m.然后用恒力向上拉,经过1s下颚到达单杠.不考虑空气阻力和因手臀穹曲而引起人的重心相对人体位置的变化,取g=1Om/s2.则该同学( )
新修订的《国家学生体质健康标准》将“引体向上”作为男同学的必测项目.如图所示.质量为50kg的某同学两手正提单杠,开始时,手臂完全伸直,身体呈自然悬垂状态,此时他的下顎距单杠面的高度为0.6m.然后用恒力向上拉,经过1s下颚到达单杠.不考虑空气阻力和因手臀穹曲而引起人的重心相对人体位置的变化,取g=1Om/s2.则该同学( )| A. | 所用恒力大小为440N | |
| B. | 所用恒力大小为560N | |
| C. | 下颚到达单红面时速度大小为0.6 m/s | |
| D. | 向上运动的过程中处于失重状态 |
17. 春晚中“开心麻花”打造的创意形体秀--“魔幻三兄弟”给观众留下了深刻的印象.表演中三演员躺在倾角为θ(约30°)的斜面上完成一系列动作,摄像机垂直斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,甲被乙和丙“竖直向上”拋出,到最高点后 恰好悬停在“空中”.已知甲的质量为m,该过程中甲上升的“高度”为h,甲与斜面间动摩擦因数为μ.设甲和斜面间最大静摩擦力等于滑动摩擦力,不计空气阻力,则( )
春晚中“开心麻花”打造的创意形体秀--“魔幻三兄弟”给观众留下了深刻的印象.表演中三演员躺在倾角为θ(约30°)的斜面上完成一系列动作,摄像机垂直斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,甲被乙和丙“竖直向上”拋出,到最高点后 恰好悬停在“空中”.已知甲的质量为m,该过程中甲上升的“高度”为h,甲与斜面间动摩擦因数为μ.设甲和斜面间最大静摩擦力等于滑动摩擦力,不计空气阻力,则( )
 春晚中“开心麻花”打造的创意形体秀--“魔幻三兄弟”给观众留下了深刻的印象.表演中三演员躺在倾角为θ(约30°)的斜面上完成一系列动作,摄像机垂直斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,甲被乙和丙“竖直向上”拋出,到最高点后 恰好悬停在“空中”.已知甲的质量为m,该过程中甲上升的“高度”为h,甲与斜面间动摩擦因数为μ.设甲和斜面间最大静摩擦力等于滑动摩擦力,不计空气阻力,则( )
春晚中“开心麻花”打造的创意形体秀--“魔幻三兄弟”给观众留下了深刻的印象.表演中三演员躺在倾角为θ(约30°)的斜面上完成一系列动作,摄像机垂直斜面拍摄,让观众产生演员在竖直墙面前表演的错觉.如图所示,甲被乙和丙“竖直向上”拋出,到最高点后 恰好悬停在“空中”.已知甲的质量为m,该过程中甲上升的“高度”为h,甲与斜面间动摩擦因数为μ.设甲和斜面间最大静摩擦力等于滑动摩擦力,不计空气阻力,则( )| A. | 甲被抛出时的速度大小为$\sqrt{2gh(sinθ-μgcosθ)}$ | |
| B. | 甲运动的时间为$\sqrt{\frac{2h}{g(sinθ+μcosθ)}}$ | |
| C. | 甲的重力势能增加了mgh | |
| D. | 乙和丙对甲做的功为mgh(sinθ+μcosθ) |
7.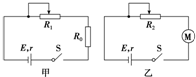 如图所示,电源电动势E=12V,内阻r=3Ω,R0=1Ω,直流电动机内阻 R0′=1Ω,当调节滑动变阻器R1时可使 甲电路输出功率最大,调节R2时可使乙 电路输出功率最大,且此时电动机刚好正常工作(额定输出功率为P0=2W),甲图电流为I1,乙图电流为I2,则下列选项正确的是( )
如图所示,电源电动势E=12V,内阻r=3Ω,R0=1Ω,直流电动机内阻 R0′=1Ω,当调节滑动变阻器R1时可使 甲电路输出功率最大,调节R2时可使乙 电路输出功率最大,且此时电动机刚好正常工作(额定输出功率为P0=2W),甲图电流为I1,乙图电流为I2,则下列选项正确的是( )
 如图所示,电源电动势E=12V,内阻r=3Ω,R0=1Ω,直流电动机内阻 R0′=1Ω,当调节滑动变阻器R1时可使 甲电路输出功率最大,调节R2时可使乙 电路输出功率最大,且此时电动机刚好正常工作(额定输出功率为P0=2W),甲图电流为I1,乙图电流为I2,则下列选项正确的是( )
如图所示,电源电动势E=12V,内阻r=3Ω,R0=1Ω,直流电动机内阻 R0′=1Ω,当调节滑动变阻器R1时可使 甲电路输出功率最大,调节R2时可使乙 电路输出功率最大,且此时电动机刚好正常工作(额定输出功率为P0=2W),甲图电流为I1,乙图电流为I2,则下列选项正确的是( )| A. | R1=2Ω,R2=2Ω | B. | I1=2A,I2=2A | C. | R1=2Ω,R2=1.5Ω | D. | I1=2A,I2=1A |
14. 如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
 如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )
如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、$\frac{L}{2}$为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称.下列判断正确的是( )| A. | b、d两点处的电势不相同 | |
| B. | b、d两点处的电场强度相同 | |
| C. | 四点中c点处的电势最低 | |
| D. | 将一试探电荷+q沿圆周由a点移至c点,+q的电势能减小 |
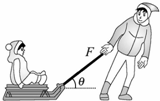 如图所示,质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面向右匀速运动(sin37°=0.6,cos37°=0.8,g=10N/kg),求:
如图所示,质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面向右匀速运动(sin37°=0.6,cos37°=0.8,g=10N/kg),求: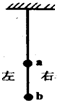 用轻质细线把两个质量未知的小球悬挂起来,如图所示.今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大的恒力,最后达到平衡,表示平衡状态的图可能是图中的哪一种?( )
用轻质细线把两个质量未知的小球悬挂起来,如图所示.今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大的恒力,最后达到平衡,表示平衡状态的图可能是图中的哪一种?( )


