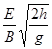题目内容
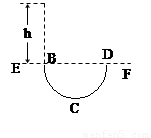
 如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B,一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出,下列说法正确的是( )
如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B,一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出,下列说法正确的是( )A.微粒受到电场力的方向一定竖直向下
B.微粒做圆周运动的半径为
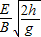
C.从B点运动到D点的过程中微粒的电势能和重力势能之和在最低点C最小
D.从B点运动到D点的过程中微粒的电势能先减小后增大
【答案】分析:带电微粒进入正交的匀强电场和匀强磁场中,受到重力、电场力和洛伦兹力而做匀速圆周运动,可知电场力与重力平衡.由洛伦兹力提供向心力,可求出微粒做圆周运动的半径.根据电场力做功正负,判断电势能的变化和机械能的变化.
解答:解:
A、由题,带电微粒进入正交的匀强电场和匀强磁场中做匀速圆周运动,电场力与重力必定平衡,则微粒受到的电场力的方向一定竖直向上.故A错误.
B、由上则有:mg=qE ①由洛伦兹力提供向心力,则有 qvB=m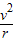 ②又v=
②又v=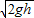 ③联立三式得,微粒做圆周运动的半径为r=
③联立三式得,微粒做圆周运动的半径为r=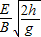 .故B正确.
.故B正确.
C、根据能量守恒定律得知:微粒在运动过程中,电势能、动能、重力势能之和一定,动能不变,则知微粒的电势能和重力势能之和一定.故C错误.
D、由于电场力方向竖直向上,则微粒从B点运动到D点的过程中,电场力先做负功后做正功,则其电势能先增大后减小.故D错误.
故选B
点评:本题解题关键是分析微粒做匀速圆周运动的受力情况,根据合力提供向心力进行判断.
解答:解:
A、由题,带电微粒进入正交的匀强电场和匀强磁场中做匀速圆周运动,电场力与重力必定平衡,则微粒受到的电场力的方向一定竖直向上.故A错误.
B、由上则有:mg=qE ①由洛伦兹力提供向心力,则有 qvB=m
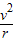 ②又v=
②又v=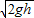 ③联立三式得,微粒做圆周运动的半径为r=
③联立三式得,微粒做圆周运动的半径为r=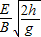 .故B正确.
.故B正确.C、根据能量守恒定律得知:微粒在运动过程中,电势能、动能、重力势能之和一定,动能不变,则知微粒的电势能和重力势能之和一定.故C错误.
D、由于电场力方向竖直向上,则微粒从B点运动到D点的过程中,电场力先做负功后做正功,则其电势能先增大后减小.故D错误.
故选B
点评:本题解题关键是分析微粒做匀速圆周运动的受力情况,根据合力提供向心力进行判断.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
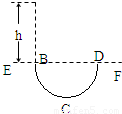
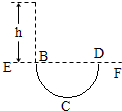 如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B.一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出. 下列说法正确的是( )
如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B.一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出. 下列说法正确的是( )| A、电场强度E的方向一定竖直向上 | ||||||
B、微粒做圆周运动的半径为
| ||||||
| C、从B点运动到D点的过程中微粒的电势能先增大后减小 | ||||||
| D、从B点运动到D点的过程中微粒的电势能和重力势能之和在最低点C最小 |
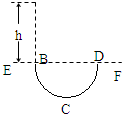 如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B,一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出,下列说法正确的是( )
如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B,一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出,下列说法正确的是( ) (2008?威海模拟)如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B.一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出.下列说法正确的是( )
(2008?威海模拟)如图所示,虚线EF的下方存在着正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B.一带电微粒自离EF为h的高处由静止下落,从B点进入场区,做了一段匀速圆周运动,从D点射出.下列说法正确的是( )