题目内容
7. 如图甲所示,一位同学利用光电计时器等器材做“验证机械能守恒定律”的实验.有一直径为d、质量为m的金属小球从A处由静止释放,下落过程中能通过A处正下方、固定于B处的光电门,测得A、B间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g.则:
如图甲所示,一位同学利用光电计时器等器材做“验证机械能守恒定律”的实验.有一直径为d、质量为m的金属小球从A处由静止释放,下落过程中能通过A处正下方、固定于B处的光电门,测得A、B间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g.则:(1)小球经过光电门B时的速度表达式为$\frac{d}{t}$.
(2)多次改变高度H,重复上述实验,作出$\frac{1}{{t}^{2}}$随H的变化图象如图乙所示,当图中已知量t0、H0和重力加速度g及小球的直径d满足表达式:2gH0${t}_{0}^{2}$=d2时,可判断小球下落过程中机械能守恒.
(3)实验中发现动能增加量△EK总是稍小于重力势能减少量△EP,增加下落高度后,则△Ep-△Ek将增加(选填“增加”、“减小”或“不变”).
分析 由题意可知,本实验采用光电门利用平均速度法求解落地时的速度;则根据机械能守恒定律可知,当减小的机械能应等于增大的动能;由原理即可明确注意事项及数据的处理等内容.
解答 解:(1)已知经过光电门时的时间小球的直径;则可以由平均速度表示经过光电门时的速度;
故v=$\frac{d}{t}$;
(2)若减小的重力势能等于增加的动能时,可以认为机械能守恒;
则有:mgH=$\frac{1}{2}$mv2;
即:2gH0=($\frac{d}{{t}_{0}}$)2
解得:2gH0${t}_{0}^{2}$=d2;
(3)由于该过程中有阻力做功,而高度越高,阻力做功越多;故增加下落高度后,则△Ep-△Ek将增大;
故答案为:(1)$\frac{d}{t}$;(2)2gH0${t}_{0}^{2}$=d2;(3)增加.
点评 考查求瞬时速度的方法,理解机械能守恒的条件,掌握分析的思维,同时本题为创新型实验,要注意通过分析题意明确实验的基本原理才能正确求解.

练习册系列答案
相关题目
17. 如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
 如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )| A. | a、c两点的电场强度相同 | |
| B. | a、c两点的电势相同 | |
| C. | 正电荷在a点的电势能大于在b点的电势能 | |
| D. | 将正电荷由O移到b电场力做正功 |
2.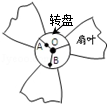 图为吊扇的简易结构图,吊扇工作时是通过吊扇上的转盘转动而带动扇叶转动来工作的.A、B是转盘上的两点,它们到转盘中心O的距离rA<rB.扇叶转动后,下列说法正确的是( )
图为吊扇的简易结构图,吊扇工作时是通过吊扇上的转盘转动而带动扇叶转动来工作的.A、B是转盘上的两点,它们到转盘中心O的距离rA<rB.扇叶转动后,下列说法正确的是( )
 图为吊扇的简易结构图,吊扇工作时是通过吊扇上的转盘转动而带动扇叶转动来工作的.A、B是转盘上的两点,它们到转盘中心O的距离rA<rB.扇叶转动后,下列说法正确的是( )
图为吊扇的简易结构图,吊扇工作时是通过吊扇上的转盘转动而带动扇叶转动来工作的.A、B是转盘上的两点,它们到转盘中心O的距离rA<rB.扇叶转动后,下列说法正确的是( )| A. | A、B两点的周期不等 | B. | A、B两点的线速度大小相等 | ||
| C. | A、B两点的角速度大小相等 | D. | A、B两点的向心加速度相等 |
12.如图,固定的光滑斜面倾角为θ,物体以初速度V0沿斜面向上滑动,恰好到达斜面的最高点A,A点离地面高度为H1.若斜面的末端点为B点、C点,物体仍以初速度V0沿斜面向上滑动,物体将飞离斜面,离开斜面后运动过程中离地的最大高度分别为H2、H3;若物体与地面成θ角以初速度V0向上斜抛,物体运动过程中离地的最大高度为H4,则下列关系式正确的是( )


| A. | H1>H2>H3>H4 | B. | H1<H2<H3<H4 | C. | H1=H2=H3=H4 | D. | H1=H2=H3>H4 |
19. 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k,做法是先将待测弹簧的一端固定在铁架台上,然后将最小分度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的钩码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记作L2;…;挂七个50g的钩码时,指针指示的刻度数值记作L7.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k,做法是先将待测弹簧的一端固定在铁架台上,然后将最小分度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的钩码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记作L2;…;挂七个50g的钩码时,指针指示的刻度数值记作L7.
(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.
测量记录表:
(2)实验中,L3和L7两个值还没有测定,请你根据上图将这两个测量值填入记录表中.
(3)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值:d4=L7-L3=7.20cm.
(4)根据以上差值,可以求出每增加50g钩码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=L7-L3,代入数据解得△L=7.20cm.(保留三位有效数字)
(5)计算弹簧的劲度系数k=28N/m(g取9.8m/s2) (保留二位有效数字)
 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k,做法是先将待测弹簧的一端固定在铁架台上,然后将最小分度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的钩码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记作L2;…;挂七个50g的钩码时,指针指示的刻度数值记作L7.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k,做法是先将待测弹簧的一端固定在铁架台上,然后将最小分度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的钩码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的钩码时,指针指示的刻度数值记作L2;…;挂七个50g的钩码时,指针指示的刻度数值记作L7.(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.
测量记录表:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
(3)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值:d4=L7-L3=7.20cm.
(4)根据以上差值,可以求出每增加50g钩码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=L7-L3,代入数据解得△L=7.20cm.(保留三位有效数字)
(5)计算弹簧的劲度系数k=28N/m(g取9.8m/s2) (保留二位有效数字)
15.在电场中的某点放一个检验电荷,其电量为q,受到的电场力为F,则该点的电场强度为E=$\frac{F}{q}$,下列说法正确的是( )
| A. | 若移去检验电荷,则该点的电场强度为0 | |
| B. | E和F无关,E和q无关 | |
| C. | 若放置到该点的检验电荷变为-2q,则场中该点的场强大小改变,方向相反 | |
| D. | 若放置到该点的检验电荷变为-2q,则场中该点的场强大小和方向均不变 |

 如图所示,质量m=1.0×103kg的汽车驶过半径R=50m的圆形拱桥,当它到达桥顶时,速度v=5.0m/s.汽车到达桥顶时对桥面的压力大小为9500N.
如图所示,质量m=1.0×103kg的汽车驶过半径R=50m的圆形拱桥,当它到达桥顶时,速度v=5.0m/s.汽车到达桥顶时对桥面的压力大小为9500N.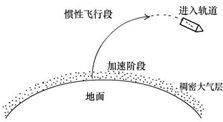 人造卫星是由运载火箭点火发射后送入其运行轨道的.其发射后的飞行过程大致可分为:垂直加速阶段,惯性飞行阶段和进入轨道阶段.如图所示:
人造卫星是由运载火箭点火发射后送入其运行轨道的.其发射后的飞行过程大致可分为:垂直加速阶段,惯性飞行阶段和进入轨道阶段.如图所示: