��Ŀ����
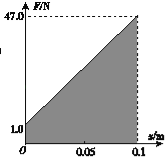
����Ŀ����ͼ��ʾ��һ�����ʵ�����˹̶���ˮƽ�����ϣ��Ҷ˷�һ������Ϊ�ʵ��С��飬С��������Ϊm=1.0kg�������ɴ���ԭ��ʱ��С��龲ֹ��O�㣬�ֶ�С���ʩ��һ��������ʹ�������ƶ���ѹ�����ɣ�ѹ����Ϊx=0.1m����A�㣬����һ�����У�����������ѹ�����Ĺ�ϵ��ͼ��ʾ��Ȼ���ͷ�С��飬��С����������˶�����֪O��������B��ľ���ΪL=2x��ˮƽ����ĸ�Ϊh=5.0m������ʱ�����û���Ħ�������Ƶ������Ħ��������gȡ10m/s2����

��1����ѹ�����ɹ����У����ɴ�������������ܣ�
��2��С��鵽������B��ʱ�ٶȵĴ�С��
��3��С�����ص�������B��ˮƽ���룮
���𰸡���1��2.3J��2��20m/s��3��1.2m
�������������������1���ڵ��ɱ�ѹ�������У���F������ת��Ϊ��Ħ������������֮�⣬���ת��Ϊ�������ܣ���˹ؼ��Ǹ�����F��ѹ�����Ĺ�ϵ��ȷ�����F���Ĺ���
��2��Ū��С������˶������������������������Ȼ����ݶ��ܶ���������⣮
��3��С���뿪�����������ƽ���˶�������ƽ���˶����ɼ�����⣮
�⣺��1����F��xͼ�п�����С���������Ķ�Ħ������СΪf="1.0" N����ѹ�������У�Ħ��������Ϊ��Wf=fx=��0.1 J
��ͼ����x�������������ͼ�����ɵ���������Ϊ��
WF=��1+47����0.1��2="2.4" J
���Ե��ɴ����ĵ�������Ϊ��EP=WF��Wf="2.3" J
�ʵ��ɴ��������������Ϊ2.3J��
��2����A�㿪ʼ��B��Ĺ����У�����L=2x��
Ħ��������ΪW��f=f3x="0.3" J
��С����ö��ܶ����У�
![]()
��ã�vB="2" m/s
��С��鵽������B��ʱ�ٶȵĴ�СΪ2m/s��
��3������B�㿪ʼ��ƽ���˶��������У�
![]() ������ʱ��t="1" s
������ʱ��t="1" s
ˮƽ����s=vBt="2" m
��С�����ص�������B��ˮƽ����Ϊ2m��

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�