Question

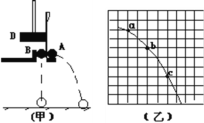
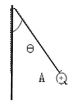
【题目】如图所示，足够长的倾斜传送带的倾角为=37°，传送带以=8 m/s的速度沿逆时针方向运动。—个半径为R =2m的光滑竖直圆弧轨道与传送带相切于传送带底端A点，B点为圆孤轨道最低点，D点为最高点。一个质量为m = l kg的小滑块P在传送带C点由静止释放，AC间距离为L=8.5 m， P与传送带之间的动摩擦因数为 =0.25。已知重力加速度取10 m/s2，sin 37°=0.6，cos37°=0.8。求：

(1)P在传送带上运动的时间；

(2)请通过计算判断P能否通过最高点，若能，求P在D点对轨道的压力。

Answer 1

【答案】(1) 1.5s (2) 4N、方向竖直向上

【解析】

（1）P从静止释放到与传送带速度相等，P做匀加速运动，根据牛顿第二定律可知，P的加速度大小为

此过程的运动时间

运动位移

之后P比传送带速度大，受到的滑动摩擦力向上，沿传送带再次向下加速运动，运动位移

P的加速度大小为

运动到底端的速度

此过程运动的时间为

运动总时间

解得

t=1.5s

（2）小滑块P通过最高点的最小速度设为，有

解得

小滑块下滑到A点的速度为，假设能经过D点且经过D点的速度为，对小滑块P应用机械能守恒定律有

解得

说明P能通过圆弧轨道最高点D。

在D点，对小滑块应用向心力公式有

再根据牛顿第三定律可知，小滑块对轨道的压力大小为

则P对轨道的压力大小为F=4N、方向竖直向上。