题目内容
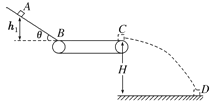
【题目】倾角![]() 的斜面底端与水平传送带平滑接触,传送带BC长L=6m,始终以
的斜面底端与水平传送带平滑接触,传送带BC长L=6m,始终以![]() 的速度顺时针运动。一个质量m=1kg的物块从距斜面底端高度
的速度顺时针运动。一个质量m=1kg的物块从距斜面底端高度![]() 的A点由静止滑下,物块通过B点时速度的大小不变。物块与斜面、物块与传送带间动摩擦因数分别为
的A点由静止滑下,物块通过B点时速度的大小不变。物块与斜面、物块与传送带间动摩擦因数分别为![]() 、
、![]() ,传送带上表面在距地面一定高度处,g取
,传送带上表面在距地面一定高度处,g取![]() 。(sin37°=0.6,cos37°=0.8)
。(sin37°=0.6,cos37°=0.8)
(1)求物块由A点运动到C点的时间;
(2)求物块距斜面底端高度满足什么条件时,将物块静止释放均落到地面上的同一点D。
【答案】(1)4s;(2)1.8m![]() h
h![]() 9m;
9m;
【解析】试题分析:(1)根据牛顿第二定律求出物块在斜面上的加速度,结合位移时间公式求出物块从A点运动到B点的时间,物块滑上传送带时,由于速度与传送带速度相等,将做匀速直线运动,结合位移和速度求出匀速运动的时间,从而得出物块由A点运动到C点的时间。(2)物块每次均抛到同一点D,由平抛知识知:物块到达C点时速度必须有![]() ,抓住两个临界状态,即滑上传送带一直做匀加速直线运动和滑上传送带一直做匀减速运动,结合动力学知识求出两种临界情况下的高度,从而得出高度的范围。
,抓住两个临界状态,即滑上传送带一直做匀加速直线运动和滑上传送带一直做匀减速运动,结合动力学知识求出两种临界情况下的高度,从而得出高度的范围。
(1)A到B,由动能定理得:![]()
得![]()
由牛顿第二定律得:![]()
得![]()
根据运动学公式得:![]()
B到C,由题可知,物块做匀速直线运动,则有![]()
A到C总时间:![]()
(2)要使物块落在地面上同一点,物块在C点速度![]()
①当距传送带底端高度为![]() 时,物块滑上传送带后一直做匀加速运动
时,物块滑上传送带后一直做匀加速运动
A到C ,由动能定理得:![]()
得![]()
②当距传送带底端高度为![]() 时,物块滑上传送带后一直做匀减速运动
时,物块滑上传送带后一直做匀减速运动
A到C ,由动能定理得:![]()
得![]()
故![]()

练习册系列答案
相关题目