题目内容

在用单摆测重力加速度的实验中：
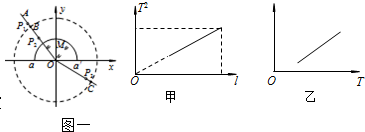
（1）某同学实验时通过改变摆线长，测出几组摆线长L和对应的周期T的数据，作出L-T2图线，如图所示．利用图线上任两点A、B的坐标（x1，y1）、（x2，y2），可求得重力加速度g=
4π2
y2-y1
x2-x1
4π2
y2-y1
x2-x1
；
（2）利用L-T2图线求解重力加速度问题时，若摆球的质量分布不均匀，直线AB将
不通过
不通过
坐标原点（填“通过”、“不通过”）．
分析：根据单摆的周期公式求出摆长和周期的关系，通过图线的斜率求出重力加速度．摆球的质量不均匀，则摆长发生变化．
解答：解：根据T=2π
L
g
，得L=
gT2
4π2
，知图线的斜率为
g
4π2
，有：
g
4π2
=
y2-y1
x2-x1
，解得g=4π2
y2-y1
x2-x1
．
若摆球的质量分布不均匀，则测量的摆长不准确，但是摆长的变化量不变，图线的斜率不变，但是图线不再通过坐标原点．
故答案为：（1）4π2
y2-y1
x2-x1
（2）不通过
点评：解决本题的关键掌握实验的原理，通过周期公式得出图线的斜率的物理意义．
练习册系列答案
相关题目
在“用单摆测重力加速度”的实验中，某同学的操作步骤为：
a．取一根细线，下端系住直径为d的金属小球，上端固定在铁架台上；
b．用米尺量得细线长度l
c．在摆线偏离竖直方向5°位置释放小球
d．用秒表记录小球完成n次全振动的总时间t，得到周期T=t/n
e．用公式g=
4π2lT2
计算重力加速度
按上述方法得出的重力加速度值与实际值相比
偏小
偏小
（选填“偏大”、“相同”或“偏小”）．
在用单摆测重力加速度的实验中：用摆线长为L、摆球直径为2r的单摆测定本地的重力加速度，测得这架单摆完成N次全振动用去时间t，那么，本地的重力加速度g=
4π2N2(L+r)
t2
4π2N2(L+r)
t2
．某同学用该式求重力加速度，在计算摆长时，只测了摆线长而没有将摆球半径计算在内，最后求得的g值将比真实值
偏小
偏小
．（填“偏大”或“偏小”）．
在“用单摆测重力加速度”的实验中，
（1）某同学的操作步骤为：
a．取一根细线，下端系住直径为d的金属小球，上端固定在铁架台上
b．用米尺量得细线长度l
c．在摆线偏离竖直方向5°位置释放小球
d．用秒表记录小球完成n次全振动的总时间t，得到周期T=
t
n

e．用公式g=
4π2l
T2
计算重力加速度
按上述方法得出的重力加速度值与实际值相比
偏小
偏小
（选填“偏大”、“相同”或“偏小”）．
（2）已知单摆在任意摆角θ时的周期公式可近似为T′=T0[1+asin2(
θ
2
)]，式中T0为摆角趋近于0°时的周期，a为常数．为了用图象法验证该关系式，需要测量的物理量有
啊T′（或t、n）、θ
啊T′（或t、n）、θ
；若某同学在实验中得到了如图甲所示的图线，则图象中的横轴表示
T
′
 
T
′
 
．
（3）某同学利用如图乙所示的实验装置验证机械能守恒定律，弧形轨道末端水平，离地面的高度为H，将钢球从轨道的不同高度h处静止释放，钢球的落点距轨道末端的水平距离为s．
1）若轨道完全光滑，s2与h的理论关系应满足s2=
4gH
4gH
（用H、h表示）．
2）该同学经实验测量得到一组数据，如表所示：
h（10-1m） 2.00 3.00 4.00 5.00 6.00
s2（10-1m2） 2.62 3.89 5.20 6.53 7.78
请在坐标纸上作出s2-h关系图．
3）对比实验结果与理论计算得到的s2-h关系图线（图丙中已画出），自同一高度静止释放的钢球，水平抛出的速率
小于
小于
（填“小于”或“大于”）理论值．
4）从s2-h关系图线中分析得出钢球水平抛出的速率差十分显著，你认为造成上述偏差的可能原因是
摩擦、转动（回答任一个即可）
摩擦、转动（回答任一个即可）
．
（1）在“用单摆测重力加速度”的实验中，下列措施中可以提高实验精度的是
ABC
ABC
．
A．选细线做为摆线
B．单摆摆动时保持摆线在同一竖直平面内
C．拴好摆球后，令其自然下垂时测量摆长
D．计时起止时刻，选在最大摆角处
（2）某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为97.50cm，摆球直径为2.00cm，然后用秒表记录了单摆振动50次所用的时间，则：
①该摆摆长为
98.50
98.50
 cm．
②如果测得的g值偏小，可能的原因是
B
B
．
A．测摆线长时摆线拉得过紧
B．摆线上端悬点末固定，振动中出现松动，使摆线长度增加了
C．开始计时时，秒表过迟按下
D．实验中误将49次全振动记为50次
③为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l与T的数据，再以l为横坐标，T2为纵坐标，将所得数据连成直线如图所示，并求得该直线的斜率为k，则重力加速度g=
4π2
k
4π2
k
（用k表示）．
（1）某同学用半圆形玻璃砖测定玻璃的折射率（如图所示）．实验的主要过程如下：
a．把白纸用图钉钉在木板上，在白纸上作出直角坐标系xOy，在白纸上画一条线段 AO表示入射光线．
b．把半圆形玻璃砖M放在白纸上，使其底边aa′与Ox轴重合．
c．用一束平行于纸面的激光从y＞0区域沿y轴负方向射向玻璃砖，并沿x轴方向调整玻璃砖的位置，使这束激光从玻璃砖底面射出后，仍沿y轴负方向传播．
d．在AO线段上竖直地插上两枚大头针P1、P2．
e．在坐标系的y＜0的区域内竖直地插上大头针P3，并使得从P3一侧向玻璃砖方向看去，P3能同时挡住观察P1和P2的视线．
f．移开玻璃砖，作OP3连线，用圆规以O点为圆心画一个圆（如图中虚线所示），此圆与AO线交点为B，与OP3连线的交点为C．确定出B点到x轴、y轴的距离分别为x1、y1、，C点到x轴、y轴的距离分别为x2、y2．
①根据上述所确定出的B、C两点到两坐标轴的距离，可知此玻璃折射率测量值的表达式为n=
 
．
②若实验中该同学在y＜0的区域内，从任何角度都无法透过玻璃砖看到P1、P2，其原因可能是：
 
．
（2）在“用单摆测重力加速度”的实验中，某同学的主要操作步骤如下：
a．取一根符合实验要求的摆线，下端系一金属小球，上端固定在O点；
b．在小球静止悬挂时测量出O点到小球球心的距离l；
c．拉动小球使细线偏离竖直方向一个不大的角度（约为5°），然后由静止释放小球；
d．用秒表记录小球完成n次全振动所用的时间t．
①用所测物理量的符号表示重力加速度的测量值，其表达式为g=
 
；
②若测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是
 
．（选填下列选项前的序号）
A．测量摆长时，把摆线的长度当成了摆长
B．摆线上端未牢固地固定于O点，振动中出现松动，使摆线越摆越长
C．测量周期时，误将摆球（n-1）次全振动的时间t记为了n次全振动的时间，并由计算式T=t/n求得周期
D．摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后，为了减小实验误差，他决定用图象法处理数据，并通过改变摆长，测得了多组摆长l和对应的周期T，并用这些数据作出T2-l图象如图甲所示．若图线的斜率为k，则重力加速度的测量值g=
 
．
④这位同学查阅资料得知，单摆在最大摆角θ较大时周期公式可近似表述为T=2π
l
g
（1+
1
4
sin2
θ
2
）．为了用图象法验证单摆周期T和最大摆角θ的关系，他测出摆长为l的同一单摆在不同最大摆角θ时的周期T，并根据实验数据描绘出如图乙所示的图线．根据周期公式可知，图乙中的纵轴表示的是
 
，图线延长后与横轴交点的横坐标为
 
．
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网