题目内容
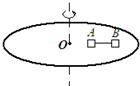 如图所示,水平转盘可绕过O点的竖直轴转动.转盘的同一半径上放有质量均为0.4kg的小物块A、B (可看成质点),A与转轴间距离为0.1m,A、B间用长0.1m的细线相连,A、B与水平转盘间最大静摩擦力均为0.54N,g取10m/s2.则当转盘转动的角速度为
如图所示,水平转盘可绕过O点的竖直轴转动.转盘的同一半径上放有质量均为0.4kg的小物块A、B (可看成质点),A与转轴间距离为0.1m,A、B间用长0.1m的细线相连,A、B与水平转盘间最大静摩擦力均为0.54N,g取10m/s2.则当转盘转动的角速度为分析:当转台的角速度比较小时,A、B物块做圆周运动的向心力由静摩擦力提供,随着角速度增大,由Fn=mω2r知向心力增大,由于B物块的转动半径大于A物块的转动半径,B物块的静摩擦力先达到最大静摩擦力,角速度再增大,则细线上出现张力,角速度继续增大,A物块受的静摩擦力也将达最大,这时A物块开始滑动.
解答:解:根据fm=mrω2知:ω=
.
知B物体先达到最大静摩擦力,则:
ω=
rad/s=
rad/s.
当ω继续增大,A受静摩擦力也达到最大静摩擦力时,A开始滑动,设这时的角速度为ω1,对A物块有:
Ffm-FT=m
ω12
对B物块有:
Ffm+FT=mω12r,
联立两式解得:
ω1=
=
rad/s=3rad/s.
故答案为:
,3.
|
知B物体先达到最大静摩擦力,则:
ω=
|
3
| ||
| 2 |
当ω继续增大,A受静摩擦力也达到最大静摩擦力时,A开始滑动,设这时的角速度为ω1,对A物块有:
Ffm-FT=m
| r |
| 2 |
对B物块有:
Ffm+FT=mω12r,
联立两式解得:
ω1=
|
|
故答案为:
3
| ||
| 2 |
点评:本题的关键是抓住临界状态,隔离物体,正确受力分析,根据牛顿第二定律求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
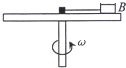 如图所示,水平转盘可绕竖直中心轴转动,盘上放着质量为1kg的B物块,B物块用长为0.25m的细线与固定在转盘中心处的力传感器相连,物块和传感器的大小均可不计.细线能承受的最大拉力为8N.B与转盘间的最大静摩擦力为4N.转盘静止时,细线刚好伸直,传感器的读数为零.当转盘以不同的角速度匀速转动时,求:(g取10m/s2)
如图所示,水平转盘可绕竖直中心轴转动,盘上放着质量为1kg的B物块,B物块用长为0.25m的细线与固定在转盘中心处的力传感器相连,物块和传感器的大小均可不计.细线能承受的最大拉力为8N.B与转盘间的最大静摩擦力为4N.转盘静止时,细线刚好伸直,传感器的读数为零.当转盘以不同的角速度匀速转动时,求:(g取10m/s2) 如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m的小球A和B.现将A和B分别置于距轴x和2x处,并用不可伸长的轻绳相连.已知两球与杆之间的最大静摩擦力都是fm.试分析转速ω从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,ω与m、x、fm的关系式.
如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m的小球A和B.现将A和B分别置于距轴x和2x处,并用不可伸长的轻绳相连.已知两球与杆之间的最大静摩擦力都是fm.试分析转速ω从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,ω与m、x、fm的关系式.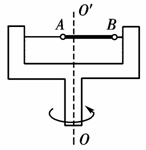
 的小球A和B。现将A和B分别置于距轴
的小球A和B。现将A和B分别置于距轴 和
和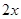 处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是
处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是 。试分析转速
。试分析转速 从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,
从零逐渐增大,两球对轴保持相对静止过程中,在满足下列条件下,