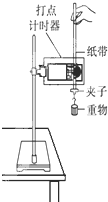
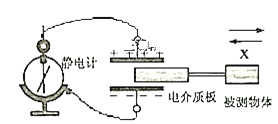
��Ŀ����
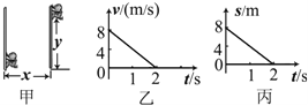
����Ŀ��һС�����б����A���ɾ�ֹ�ͷţ�����ʱ��4t0����B������5t0ʱ�̻����˶���ˮƽ���C��ֹͣ��������б���ˮƽ���Ķ�Ħ��������ͬ����֪�������˶���������Ӵ�����Ħ������С��ʱ��Ĺ�ϵ��ͼ��ʾ���軬���˶���B��ǰ�����ʲ��䣮����˵������ȷ����(�� ��)
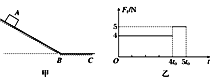
A. ������б���ˮƽ���ϵ�λ�ƴ�С֮��Ϊ16��5
B. ������б���ˮƽ���ϵļ��ٶȴ�С֮��Ϊ1��4
C. б������Ϊ45��
D. ������б��Ķ�Ħ����������![]()
���𰸡�BD
��������
��������б���ϼ��٣�����ˮƽ���ϼ��٣�B����ٶȴ�С����ͬ�ģ������ͼ�е�ʱ���ϵ�����ɵó����ٶȵĹ�ϵ���ɼ��ٶ���ʱ��Ĺ�ϵ������˶�ѧ�Ĺ�ʽ�������λ�ƹ�ϵ������ͼ�ó��ܵ���Ħ�����Ĺ�ϵ���Ӷ��ó�б�����ǣ����������б�����������������ţ�ٵڶ��������Ħ��������
�軬������B����ٶ�Ϊv��������б���ϵ�λ�ƣ�x1=![]() 4t0����ˮƽ���ϵ�λ�ƣ�x2=
4t0����ˮƽ���ϵ�λ�ƣ�x2=![]() t0��������б���ˮƽ���λ�ƴ�С֮�ȣ�
t0��������б���ˮƽ���λ�ƴ�С֮�ȣ� ����A������A��B�Ĺ����У�a14t0=v��B��C�Ĺ����У�v=a2t0�����ٶ�֮�ȣ�
����A������A��B�Ĺ����У�a14t0=v��B��C�Ĺ����У�v=a2t0�����ٶ�֮�ȣ�![]() ����B��ȷ����ͼ�ҿɵã�f2=��mg=5N��f1=��mgcos��=4N�����ԣ�
����B��ȷ����ͼ�ҿɵã�f2=��mg=5N��f1=��mgcos��=4N�����ԣ�![]() ��������=370����C����������б�����˶��Ĺ����У�mgsin��-��mgcos��=ma1����ˮƽ�����˶��Ĺ����У�ma2=��mg����ã���=4/7����D��ȷ����ѡBD��
��������=370����C����������б�����˶��Ĺ����У�mgsin��-��mgcos��=ma1����ˮƽ�����˶��Ĺ����У�ma2=��mg����ã���=4/7����D��ȷ����ѡBD��

 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д�