��Ŀ����
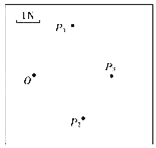
����Ŀ��CD��EF��ˮƽ���õĵ���ɺ��ԵĹ⻬ƽ�н������죬���������ˮƽ����߶�ΪH��������ΪL����ˮƽ����������ڷ���ֱ����ƽ�����ϵ��н���ǿ�ų����ų�����ΪCPQE�����Ÿ�Ӧǿ�ȴ�СΪB����ͼ��ʾ�����������һ�����Ĺ⻬���ƽ�����ӣ������Ĺ⻬������϶˽���һ����R����һ��ֵҲΪR�ĵ��������������Ͼ���ˮƽ��������߶�h���ɾ�ֹ�ͷţ����������ͨ���ų���������ˮƽ�����Ͼ���ˮƽ�������Ҷ�ˮƽ����x������֪���������Ϊm,������뵼��ʼ�սӴ����ã��������ٶ�Ϊg����

(1)����R�е���������������·�в����Ľ����ȡ�
(2)�ų�����ij���d��
���𰸡�(1) ![]() (2)
(2) 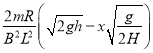
���������������: ��1���ɻ�е���غ㶨�ɼ������ų����ٶȴ�С���ٸ��ݷ����ڵ�Ÿ�Ӧ���ɺͱպϵ�·��ŷķ����������ǿ�ȣ�����ƽ���˶���֪ʶ����ƽ���˶��ij��ٶȣ��ٸ��������غ㶨�ɼ���������·�в����Ľ����ȣ���2����ţ�ٵڶ����ɵõ�����������ٶȹ�ϵ������Ԫ�����ų�����ij��ȣ�
��1���������֪��������ս���ų���˲���ٶ�������ĸ�Ӧ�綯�����Ӧ�������
�ɻ�е���غ㶨������ ![]()
����� ![]()
�ɷ����ڵ�Ÿ�Ӧ���ɵ��� ![]()
�ɱպϵ�·ŷķ���ɵ��� ![]()
��������� ![]()
��ƽ���˶����ɿɵ��� ![]()
����� ![]()
�������غ㶨�ɿ�֪������·�в����Ľ�����Ϊ�� ![]()
��2�������ͨ���ų�����ʱ�ڰ������������������˶�
��ţ�ٵڶ����ɵã�BIL=ma����![]() ��
�� ![]()
��������� ![]()
������͵��� ![]()
��![]()
����ã� ![]()
��ã�