题目内容
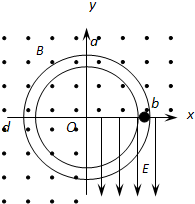 如图所示,一光滑绝缘圆管轨道位于竖直平面内,半径为0.2m.以圆管圆心O为原点,在环面内建立平面直角坐标系xOy,在第四象限加一竖直向下的匀强电场,其他象限加垂直于环面向外的匀强磁场.一带电量为+1.0C、质量为0.1kg的小球(直径略小于圆管直径),从x坐标轴上的b点由静止释放,小球刚好能顺时针沿圆管轨道做圆周运动.(重力加速度g取10m/s2)
如图所示,一光滑绝缘圆管轨道位于竖直平面内,半径为0.2m.以圆管圆心O为原点,在环面内建立平面直角坐标系xOy,在第四象限加一竖直向下的匀强电场,其他象限加垂直于环面向外的匀强磁场.一带电量为+1.0C、质量为0.1kg的小球(直径略小于圆管直径),从x坐标轴上的b点由静止释放,小球刚好能顺时针沿圆管轨道做圆周运动.(重力加速度g取10m/s2)(1)求匀强电场的电场强度E;
(2)若第二次到达最高点a时,小球对轨道恰好无压力,求磁感应强度B;
(3)求小球第三次到达最高点a时对圆管的压力.
分析:(1)因为小球刚好能绕圆管做圆周运动,则在最高点的速度为零,根据动能定理求出匀强电场的电场强度.
(2)根据动能定理求出第二次到达最高点的速度,抓住重力和洛伦兹力的合力提供向心力求出磁感应强度的大小.
(3)根据动能定理求出第三次到达最高点的速度,根据径向的合力提供向心力求出圆管对小球的作用力,从而得出小球对圆管的压力.
(2)根据动能定理求出第二次到达最高点的速度,抓住重力和洛伦兹力的合力提供向心力求出磁感应强度的大小.
(3)根据动能定理求出第三次到达最高点的速度,根据径向的合力提供向心力求出圆管对小球的作用力,从而得出小球对圆管的压力.
解答:解:(1)小球第一次刚好过最高点,此时速度v1=0
根据动能定理得,qER-mgR=0
∴E=
=1N/C
(2)小球第二次过最高点是速度为v2,由动能定理可知2qER-mgR=
m
又 mg+qv2B=m
.
以上两式可解得 B=
=0.5T
(3)小球第三次过最高点时速度为,小球受圆管向下的压力为FN
3qER-mgR=
m
mg+qv3B+FN=m
解得 FN=(3-
)mg=(3-
)N
根据牛顿第三定律可知
小球第三次到达最高点a时对圆管的压力为(3-
)N 方向竖直向上.
答:(1)匀强电场的电场强度为1N/C.(2)磁感应强度B为0.5T.(3)小球第三次到达最高点a时对圆管的压力为(3-
)N,方向竖直向上.
根据动能定理得,qER-mgR=0
∴E=
| mg |
| q |
(2)小球第二次过最高点是速度为v2,由动能定理可知2qER-mgR=
| 1 |
| 2 |
| v | 2 2 |
又 mg+qv2B=m
| ||
| R |
以上两式可解得 B=
| m |
| q |
|
(3)小球第三次过最高点时速度为,小球受圆管向下的压力为FN
3qER-mgR=
| 1 |
| 2 |
| v | 2 3 |
mg+qv3B+FN=m
| ||
| R |
解得 FN=(3-
| 2 |
| 2 |
根据牛顿第三定律可知
小球第三次到达最高点a时对圆管的压力为(3-
| 2 |
答:(1)匀强电场的电场强度为1N/C.(2)磁感应强度B为0.5T.(3)小球第三次到达最高点a时对圆管的压力为(3-
| 2 |
点评:解决本题的关键知道小球做圆周运动向心力的来源,结合动能定理和牛顿第二定律进行求解.

练习册系列答案
相关题目
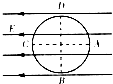 如图所示,一光滑绝缘圆环竖直放在水平向左的匀强电场E中,环上套一质量为m,带正电q的小球,qE<mg,AC是环在水平方向的直径,BD是环在竖直方向的直径,把小球从A点由静止释放,则( )
如图所示,一光滑绝缘圆环竖直放在水平向左的匀强电场E中,环上套一质量为m,带正电q的小球,qE<mg,AC是环在水平方向的直径,BD是环在竖直方向的直径,把小球从A点由静止释放,则( )| A、小球速度最大的位置在B点 | B、小球对机械能最大的位置在BC间某处 | C、小球所能达到的最高点在CD间某处 | D、小球所能达到的最高点在D点 |
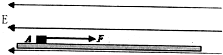 如图所示,一光滑绝缘水平木板(木板足够长)固定在水平向左、电场强度为E的匀强电场中,一电量为q(带正电)的物体在水平恒力F作用下从A点由静止开始向右加速运动,经一段时间t撤去这个力,又经时间2t物体返回A点,则( )
如图所示,一光滑绝缘水平木板(木板足够长)固定在水平向左、电场强度为E的匀强电场中,一电量为q(带正电)的物体在水平恒力F作用下从A点由静止开始向右加速运动,经一段时间t撤去这个力,又经时间2t物体返回A点,则( )| A、这一过程中带电物快的电势能先增加后减小,其变化量为0 | B、水平恒力与电场力的比为9:5 | C、水平恒力与电场力的比为7:3 | D、物快先向右加速到最右端,然后向左加速返回到A点 |
 如图所示,一光滑绝缘斜槽放在方向竖直向下、电场强度为E的匀强电场中,从斜槽顶端A沿斜槽向下释放一初速度为v0的带负电的小球,小球质量为m,带电荷量为q,斜槽底端B与A点的竖直距离为h.则关于小球的情况,下列说法中正确的是( )
如图所示,一光滑绝缘斜槽放在方向竖直向下、电场强度为E的匀强电场中,从斜槽顶端A沿斜槽向下释放一初速度为v0的带负电的小球,小球质量为m,带电荷量为q,斜槽底端B与A点的竖直距离为h.则关于小球的情况,下列说法中正确的是( )
 ,小球才能沿斜槽运动到B点
,小球才能沿斜槽运动到B点 ,小球才能沿斜槽运动到B点
,小球才能沿斜槽运动到B点