��Ŀ����
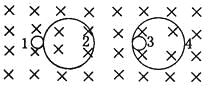
����Ŀ����ͼ��ʾ�����Ϊ������Ħ������Ϊ![]() ���㹻���ֲ�б��
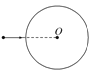
���㹻���ֲ�б��![]() ���ڱڹ⻬����ֱԲ���ι��
���ڱڹ⻬����ֱԲ���ι��![]() ������B�㣬Բ������İ뾶ΪR��
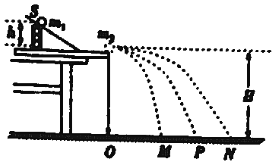
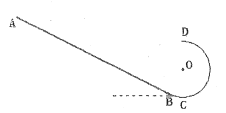
������B�㣬Բ������İ뾶ΪR��![]() ����ΪԲ���������ֱֱ��������������������Ϊm����ͬС����Ϊ�ʵ㣩���Ҿ�ֹ��C�㴦�����״�б����ij�����ٶ��ͷţ��ס�����C�㷢��������ճ��һ�𣬴˺�ǡ��ͨ��Բ�����ߵ�D����:
����ΪԲ���������ֱֱ��������������������Ϊm����ͬС����Ϊ�ʵ㣩���Ҿ�ֹ��C�㴦�����״�б����ij�����ٶ��ͷţ��ס�����C�㷢��������ճ��һ�𣬴˺�ǡ��ͨ��Բ�����ߵ�D����:
��1��С���������ײǰ˲����ٶȴ�С��
��2��С�����б�����˶���λ�ƴ�С��
���𰸡���1��![]() ����2��
����2��![]()
��������
��1�������������C����ײ�������غ㣬���������ײǰ���ٶ�Ϊ![]() ������
������
![]()
����������պ����˶���D�㣬��D�㣬�У�![]()
��C��D���ɻ�е���غ㶨�ɵã�![]()
��������ʽ�ӽ�ã�![]()
��2���Լ���A��C���ɶ��ܶ����ã�![]()
R��1��cos����+sABsin����h
��ã�![]()

��ϰ��ϵ�д�
�����Ŀ