Question

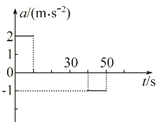
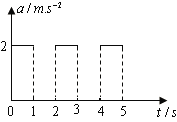
【题目】质点A沿直线以vA=5m/s匀速运动，某时刻（t=0）在A后面与A相距△x=7.75m的质点B由静止开始起动，质点B运动方向与A一致，其加速度随时间周期性变化，加速度随时间变化的图象如图所示．求：

（1）质点B追上A之前两者间的最大距离；

（2）B出发后经多少时间追上A？

Answer 1

【答案】（1）18m（2）10.5s

【解析】试题分析：当两质点的速度相等时，A、B之间的距离最大，根据速度时间公式，结合图象得出A、B距离最大的时间．通过A、B的位移求出A、B之间的最大距离．结合A、B两质点位移关系，运用运动学公式求出追及的时间．

（1）质点B的速度为5m/s时，A、B之间的距离最大，设质点B速度达到5m/s若一直做匀加速，总共需要的时间为，由运动学公式

由质点B加速度与时间关系知，经过时间时，A、B之间的距离最大．

在时间内质点A发生的位移，
质点B在第1s内的位移

质点B在第2s内的位移，式中，代入数据得．
质点B在第3s内的位移

质点B在第ns（n为整数）内的位移质点B在时间内的位移

故A、B之间的最大距离．

（2）设经历时间t（t为正整数）B追上A时间t内A的位移
时间t内B的位移，

，此式无整数解，但可求得，

10s内A发生的位移，B发生的位移，

故在10s后，B需比A多发生的位移

设10s后需时间t′B追上A则，解得

故B出发后需经过时间追上A．