题目内容
15. 如图,用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船受到的阻力大小恒为f,经过A点时的速度大小为v0,小船从A点沿直线加速运动到B点经历的时间为t,A,B两点间距离为d,缆绳质量忽略不计,下列说法正确的是( )
如图,用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船受到的阻力大小恒为f,经过A点时的速度大小为v0,小船从A点沿直线加速运动到B点经历的时间为t,A,B两点间距离为d,缆绳质量忽略不计,下列说法正确的是( )| A. | 小船从A点运动到B点的全过程克服阻力做的功Wf=fd | |
| B. | 小船由A点经过B点的过程中的动能是减小的 | |
| C. | 小船由A点经过B点的过程电动机皮带轮的线速度大于小船的速度 | |
| D. | 小船经过B点时的加速度大小a=$\frac{P}{\sqrt{{m}^{2}{{v}_{0}}^{2}+2m(Pt-fd)}}$-$\frac{f}{m}$ |
分析 (1)根据功的表达式求出阻力所做的功.
(2)根据动能定理求出小船经过B点时的速度.由Ek=$\frac{1}{2}m{v}^{2}$知速度增大,动能增大,设小船经过B点时绳的拉力大小为F,绳与水平方向夹角为θ,绳的速度大小为u,根据牛顿第二定律、功率P=Fu,以及小船速度与绳子收缩速度的关系求出B点的加速度.
解答 解:A、小船从A点运动到B点克服阻力做功Wf=fd①,故A正确
B、小船从A点运动到B点,电动机牵引绳对小船做功W=Pt1 ②
由动能定理有 W-Wf=$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{0}^{2}$③
由①②③式解得 v=$\sqrt{{v}_{0}^{2}+2•\frac{p{t}_{1}-fd}{m}}$④,由Ek=$\frac{1}{2}m{v}^{2}$知速度增大,动能增大,故B错误
C、皮带轮的线速度是小船速度的沿绳方向的一分速度,v2=Vcosθ,故电动机皮带轮的线速度小于小船的速度,故C错误;
D、设小船经过B点时绳的拉力大小为F,绳与水平方向夹角为θ,绳的速度大小为u,
P=Fu ⑤
u=v1cosθ⑥
牛顿第二定律 Fcosθ-f=ma⑦
由④⑤⑥⑦得a=$\frac{P}{\sqrt{{m}^{2}{{v}_{0}}^{2}+2m(Pt-fd)}}$-$\frac{f}{m}$,故D正确;
故选:AD
点评 本题综合考查了动能定理、牛顿第二定律等知识,综合性较强,对学生能力要求较高,尤其第三问要运用到速度的分解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
7. 如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )
如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )
 如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )
如图甲所示,a、b两条直导线垂直于纸面水平放置,且通有的电流大小相等,方向如图所示,图乙中c、d是两个电荷量相等的正点电荷,O1和O2分别为两直导线和两点电荷连线的中点,在O1和O2正上方均有一电子,以较小的速度v竖直向下射出,不计电子重力.则电子( )| A. | 在乙图中将做往复运动 | |
| B. | 在甲图中将做匀加速直线运动 | |
| C. | 在乙图中向O2点运动时,加速度一定减小 | |
| D. | 在乙图中到达O2点时动能最小,电势能最大 |
4.2012年6月18日,神州九号飞船与天宫一号目标飞行器在离地面343km的近圆形轨道上成功进行了我国首次载人空间交会对接.对接轨道所处的空间存在极其稀薄的大气,下面说法正确的是( )
| A. | 为实现对接,两者运行速度的大小都应介于第一宇宙速度和第二宇宙速度之间 | |
| B. | 如不加干预,在运行一段时间后,天宫一号的动能可能会减小 | |
| C. | 如不加干预,天宫一号的轨道高度将缓慢降低 | |
| D. | 航天员在天宫一号中处于失重状态,说明航天员不受地球引力作用 |
11.以下说法正确的是( )
| A. | 水的饱和汽压随体积的升高而增大 | |
| B. | 扩散现象表明,分子在永不停息地运动 | |
| C. | 当分子间距离增大时,分子间引力增大,分子间斥力减小 | |
| D. | 一定质量的理想气体,在等压膨胀过程中,气体分子的平均动能减小 |
5. 如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动.关于这种情况下硬币的受力情况,下列说法中正确的是( )
如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动.关于这种情况下硬币的受力情况,下列说法中正确的是( )
 如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动.关于这种情况下硬币的受力情况,下列说法中正确的是( )
如图所示,水平转台上放着一枚硬币,当转台匀速转动时,硬币没有滑动.关于这种情况下硬币的受力情况,下列说法中正确的是( )| A. | 仅受重力和台面的支持力 | |
| B. | 受重力、台面的支持力、静摩擦力和向心力 | |
| C. | 受重力、台面的支持力、沿切线与速度方向相反的静摩擦力 | |
| D. | 受重力、台面的支持力、指向圆心的静摩擦力 |
3. 一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )
一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )
 一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )
一质点沿x轴做直线运动,其V-t图象如图所示.质点在v=0时位于x=5m处,开始沿x轴正向运动.当t=8s时,质点在轴上的位置为( )| A. | x=3m | B. | x=8m | C. | x=9m | D. | x=-14m |

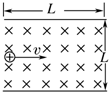 长为L的水平极板间,有垂直纸面向里的匀强磁场,如图所示,磁感应强度为B,板间距离为L,板不带电.现在质量为m、电量为q的正电粒子(不计重力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子都打在极板上,不离开磁场区域,可采用的方法是控制速度的大小,求带电粒子运动的速度范围.
长为L的水平极板间,有垂直纸面向里的匀强磁场,如图所示,磁感应强度为B,板间距离为L,板不带电.现在质量为m、电量为q的正电粒子(不计重力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子都打在极板上,不离开磁场区域,可采用的方法是控制速度的大小,求带电粒子运动的速度范围. 如图所示,理想变压器原线圈匝数 n1=140匝,副线圈总匝数 n2=1400匝,原线圈电压μ1=10V,线路电阻用R表示,R=4,用户电阻R′=16Ω.开始时滑动触头P放在副线圈的中点,不计电表对电路的影响,求:
如图所示,理想变压器原线圈匝数 n1=140匝,副线圈总匝数 n2=1400匝,原线圈电压μ1=10V,线路电阻用R表示,R=4,用户电阻R′=16Ω.开始时滑动触头P放在副线圈的中点,不计电表对电路的影响,求: