题目内容
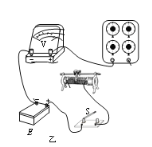
【题目】如图所示,竖直放置的圆柱形气缸固定不动,内壁光滑,下端与大气相连,A、B两活塞的面积分别为SA=20 cm2、SB=10 cm2,它们通过一条细绳连接,活塞B又与另一条细绳连接,绳子跨过两个光滑定滑轮与重物C连接.已知A、B两活塞的质量分别为 mA=2mB=1 kg,当活塞静止时,气缸中理想气体压强p1=1.2×105Pa,温度T1=800 K,活塞A距地面的高度为L=10 cm,上、下气缸内气体的长度分别为2L、L,大气压强为p0=1×105Pa,上气缸足够长,重力加速度g=10 m/s2.
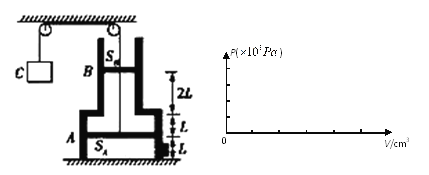
(1)求重物C的质量M;
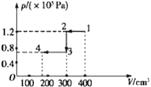
(2)缓慢降低气缸内气体的温度直至210 K,请在p-V图上画出缸内气体状态变化的图线,并计算出拐点处气体的温度及最终活塞B离地的高度。
【答案】(1)3.5 kg (2)350 K>210 K 38 cm 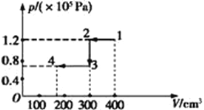
【解析】
(1)设活塞A、B间的细绳张力为T,则对活塞A、B受力分析有
p1SA+mAg=p0SA+T
p0SB+mBg+T=p1SB+Mg
联立解得M=3.5 kg
(2)刚开始降温时气缸内气体等压变化,活塞A、B均向上缓慢运动,直到A不能再上升,设此时气体温度为T2,则由盖—吕萨克定律有![]()
解得T2=600 K>210 K
此后气体再降温时,A、B间细绳张力逐渐减小至零,气体等容变化.设细绳张力为零时,气体压强为p2,温度为T3,则此时对活塞B受力分析有Mg+p2SB=p0SB+mBg
解得p2=7×104Pa
由查理定律有![]()
解得T3=350 K>210 K
之后气体等压变化,活塞A不动,活塞B下降,设B与A距离为x时,温度变化为T4=210 K,由盖—吕萨克定律有![]()
解得x=18 cm
故B离地面的高度为H=2L+x=38 cm
气缸内气体状态变化的图线如图所示.