Question

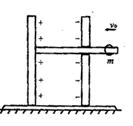
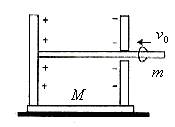
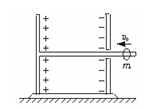
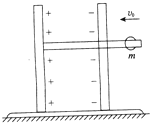如图所示，电容器固定在一绝缘座上，绝缘座放在光滑水平面上，平行板电容器板间距离为d，电容为C，右极板有一个小孔，通过小孔有一长为

3

2

d的绝缘杆，左端固定在左极板上，电容器板连同底座、绝缘杆总质量为M，给电容器充入电荷量Q后，有一质量为m的带电荷量为+q的环套在杆上以某一初速度v₀对准小孔向左运动（M=3m）．设带电环不影响电容器板间电场分布，电容器外部电场忽略不计，
带电环进入电容器后距左板最小距离为

d

2

，试求：
（1）带电环与极板间相距最近时的速度大小；
（2）若取左极板的电势为零，当环距左极板最近时环的电势能；
（3）带电环受到的电场力大小；
（4）带电环受到绝缘杆的摩擦力大小．

Answer 1

分析：选取带电环与电容器作为研究对象，根据动量守恒定律，即可求出带电环与左极扳相距最近时的速度大小；
根据电场力做功量度电势能变化求解．
再由动能定理，可求出此过程中摩擦力大小．

解答：解：（1）设环和电容器等达到共同速度v
   对m和M系统动量守恒
mv₀=（m+M）v
     v=

1

4

v₀ 
（2）根据电场力做功量度电势能变化得
环距左板最近时电势能：E=W=-q

U

2

=

-qQ

2C

 （3）根据题意得：
电场强度E=

U

d

=

Q

Cd

带电环受到的电场力大小F=

Qq

Cd

（4）设从开始到环距左板最近过程中，电容器移动距离为S，
       由动能定理，F_电S+fs=

1

2

Mv²
       对环有-F_电（S+

d

2

）-f（S+d）=

1

2

mv²-

1

2

m

v

2 0

    f=

3 mv 2 0

8d

-

Qd

2Cd

答：（1）带电环与极板间相距最近时的速度大小是

1

4

v₀；
（2）若取左极板的电势为零，当环距左极板最近时环的电势能是

-qQ

2C

；
（3）带电环受到的电场力大小是

Qq

Cd

；
（4）带电环受到绝缘杆的摩擦力大小是

3 mv 2 0

8d

-

Qd

2Cd

点评：考查动量守恒定律与动能定理的应用，注意动量守恒定律的守恒条件与方向性，并掌握动能定理的功的正负．