题目内容
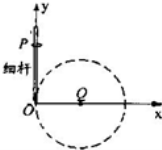
【题目】如图所示，竖直平面内的xOy坐标系中，x轴上固定一个点电荷Q，y轴上固定一根光滑绝缘细杆（细杆的下端刚好在坐标原点O处），将一个重力不计的带电圆环（可视为质点）套在杆上，从P处由静止释放，圆环从O处离开细杆后恰好绕点电荷Q做匀速圆周运动，则下列说法中正确的是（ ）
A．圆环沿细杆从P运动到O的过程中，加速度一直增大
B．圆环沿细杆从P运动到O的过程中，速度先增大后减小
C．若只增大圆环所带的电荷量，圆环离开细杆后仍能绕点电荷Q做匀速圆周运动
D．若将带电圆环从杆上P的上方由静止释放，其他条件不变，圆环离开细杆后不能绕点电荷Q做匀速圆周运动
【答案】CD
【解析】
试题分析：圆环从P运动到O的过程中，对环受力分析，环受库仑引力和杆的弹力，库仑引力沿杆方向上的分力等于圆环的合力，滑到O点时，所受的合力为零，加速度为零，故A错误；圆环从P运动到O的过程中，库仑引力做正功，动能一直增大，速度一直增大，故B错误；圆环从P运动到O的过程中，根据动能定理得，
，根据牛顿第二定律有
，可知
，轨迹半径与圆环所带电荷量无关，故C正确；若增大高度，电势差U增大，轨迹半径发生变化，圆环不能做圆周运动，故D正确。
练习册系列答案
相关题目
