题目内容
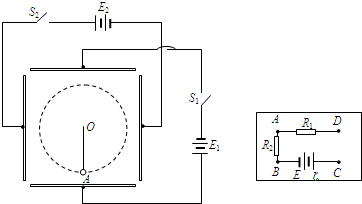 如图所示,两组完全相同的电源E1、E2分别通过开关S1、S2与两对金属板相连,每对金属板的距离均为d,如果S1、S2分别闭合能够在金属板相对的空间内建立起竖直和水平方向的匀强电场.一长为l的绝缘细线一端固定在O点,另一端栓着一个质量为m、带有一定电量q的小球,原来S1、S2都断开,小球在最低点A点处于静止状态.问:
如图所示,两组完全相同的电源E1、E2分别通过开关S1、S2与两对金属板相连,每对金属板的距离均为d,如果S1、S2分别闭合能够在金属板相对的空间内建立起竖直和水平方向的匀强电场.一长为l的绝缘细线一端固定在O点,另一端栓着一个质量为m、带有一定电量q的小球,原来S1、S2都断开,小球在最低点A点处于静止状态.问:(1)若只将S1闭合并给小球一冲量,它可在竖直平面内绕O点做匀速圆周运动,那么小球带何种电荷?电源的电动势E1等于多少?
(2)若只将S2闭合,小球从A点由静止释放,那么,运动过程中细线所受的最大拉力是多少?并在图中标明此时小球的位置.
(3)若只将S2闭合,要使小球从A点开始在竖直平面内做完整的圆周运动,至少在A点给小球多大的瞬时冲量?(已知当地的重力加速度为g)
分析:(1)可在竖直平面内绕O点做匀速圆周运动,说明小球受到的重力与电场力始终平衡,故小球必带正电.根据平衡条件,可解得电源的电动势E1.
(2)只将S2闭合,由合场的观点分析知,小球在细线与竖直方向偏右下方为45°时的D点拉力T最大(设为TM).
在D点细线与电场力和重力的合力提供向心力TM-
mg=m
,从A到D过程,运用动能定理-mgl(1-cos45°)+q
lsin45°=
mvD2,化简可解得细线所受的最大拉力TM.
(3)由合场的观点分析知,小球应在圆周上与D点对称的C点时最容易离轨,即C点为合场中的等效最高点,在C点重力和电场力的合力恰好提供向心力
mg=m
从A到C运用动能定理-mgl(1+cos45°)-q
lsin45°=
mvmin2-
mvA2,由上面二式解得vA,所以I=mvA,代入数据可得瞬时冲量I.
(2)只将S2闭合,由合场的观点分析知,小球在细线与竖直方向偏右下方为45°时的D点拉力T最大(设为TM).
在D点细线与电场力和重力的合力提供向心力TM-
| 2 |
| vD2 |
| l |
| E1 |
| d |
| 1 |
| 2 |
(3)由合场的观点分析知,小球应在圆周上与D点对称的C点时最容易离轨,即C点为合场中的等效最高点,在C点重力和电场力的合力恰好提供向心力
| 2 |
| vmin2 |
| l |
从A到C运用动能定理-mgl(1+cos45°)-q
| E1 |
| d |
| 1 |
| 2 |
| 1 |
| 2 |
解答: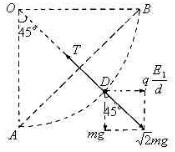 解:(1)由题意分析知:小球必带正电.
解:(1)由题意分析知:小球必带正电.
小球受到的重力与电场力始终平衡,即:
q
=mg
所以E1=
.
(2)只将S2闭合,由题意分析可知,由合场的观点分析知,小球在细线与竖直方向偏右下方为45°时的D点拉力T最大(设为TM),受力如图所示:
在D点细线与电场力和重力的合力提供向心力TM-
mg=m
从A到D过程,运用动能定理-mgl(1-cos45°)+q
lsin45°=
mvD2
由以上二式可解得:TM=(3
-2)mg.
(3)设至少给球的冲量为I,此时对应的速度为vA,
如下图所示,由合场的观点分析知,小球应在圆周上与D点对称的C点时最容易离轨,即C点为合场中的等效最高点,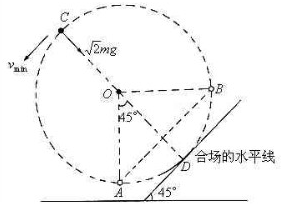
在C点重力和电场力的合力恰好提供向心力
mg=m
从A到C运用动能定理-mgl(1+cos45°)-q
lsin45°=
mvmin2-
mvA2
由上面二式解得vA=
所以I=mvA=m
.
答:(1)若只将S1闭合并给小球一冲量,它可在竖直平面内绕O点做匀速圆周运动,那么小球带正电,电源的电动势E1等于
.
(2)若只将S2闭合,小球从A点由静止释放,那么,运动过程中细线所受的最大拉力是(3
-2)mg,此时小球的位置如图所示.
(3)若只将S2闭合,要使小球从A点开始在竖直平面内做完整的圆周运动,至少在A点给小球m
的瞬时冲量.
 解:(1)由题意分析知:小球必带正电.
解:(1)由题意分析知:小球必带正电.小球受到的重力与电场力始终平衡,即:
q
| E1 |
| d |
所以E1=
| mgd |
| q |
(2)只将S2闭合,由题意分析可知,由合场的观点分析知,小球在细线与竖直方向偏右下方为45°时的D点拉力T最大(设为TM),受力如图所示:
在D点细线与电场力和重力的合力提供向心力TM-
| 2 |
| vD2 |
| l |
从A到D过程,运用动能定理-mgl(1-cos45°)+q
| E1 |
| d |
| 1 |
| 2 |
由以上二式可解得:TM=(3
| 2 |
(3)设至少给球的冲量为I,此时对应的速度为vA,
如下图所示,由合场的观点分析知,小球应在圆周上与D点对称的C点时最容易离轨,即C点为合场中的等效最高点,

在C点重力和电场力的合力恰好提供向心力
| 2 |
| vmin2 |
| l |
从A到C运用动能定理-mgl(1+cos45°)-q
| E1 |
| d |
| 1 |
| 2 |
| 1 |
| 2 |
由上面二式解得vA=
gl(3
|
所以I=mvA=m
gl(3
|
答:(1)若只将S1闭合并给小球一冲量,它可在竖直平面内绕O点做匀速圆周运动,那么小球带正电,电源的电动势E1等于
| mgd |
| q |
(2)若只将S2闭合,小球从A点由静止释放,那么,运动过程中细线所受的最大拉力是(3
| 2 |
(3)若只将S2闭合,要使小球从A点开始在竖直平面内做完整的圆周运动,至少在A点给小球m
gl(3
|
点评:此题考查了重力场合电场两个复合场中的圆周运动的问题,同时要结合牛顿第二定律和动能定理的知识分析、解决问题,是一道非常好的题目,但是综合能力要求较高,难度较大,属于难题.

练习册系列答案
相关题目