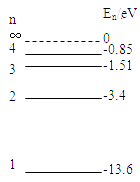题目内容
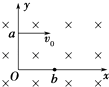
【题目】如图所示,在x轴下方的区域内存在+y方向的匀强电场,电场强度为E.在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xoy平面向外,磁感应强度为B.﹣y轴上的A点与O点的距离为d,一个质量为m、电荷量为q的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场,不计粒子的重力.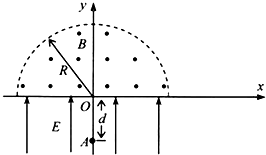
(1)求粒子在磁场中运动的轨道半径r;
(2)要使粒子进人磁场之后不再经过x轴,求电场强度的取值范围;
(3)改变电场强度,使得粒子经过x轴时与x轴成θ=300的夹角,求此时粒子在磁场中的运动时间t及经过x轴的位置坐标值x0 .
【答案】
(1)解:粒子在电场中加速,由动能定理得: ![]() ①
①
粒子进入磁场后做圆周运动,有: ![]() ②
②
解得粒子在磁场中运动的半径:r= ![]() ③
③
答:粒子在磁场中运动的轨道半径r为 ![]() ;
;
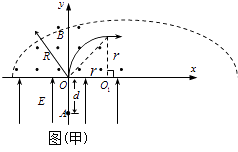
(2)解:设场强为E0时,粒子离开磁场后恰好不再经过x轴,则离开磁
场时的速度方向与x轴平行,运动情况如图(甲),易得:
![]() ④
④
由③、④式解得: ![]()
因此,场强的范围:E≥E0
即: ![]() ⑥
⑥
答:要使粒子进人磁场之后不再经过x轴,电场强度的取值范围为 ![]() ;
;
(3)解:粒子运动情况如图(乙),由几何关系可得:
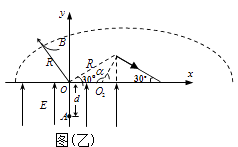
α=120° ⑦
粒子在磁场中的运动周期为: ![]() ⑧
⑧
粒子在磁场中的运动周期为:t= ![]() ⑨
⑨
联立②⑥⑦⑧可得:t= ![]() ⑩
⑩
由图可得粒子经过x轴时的位置横坐标值为:x0=2Rcos30°= ![]()
答:改变电场强度,使得粒子经过x轴时与x轴成θ=300的夹角,此时粒子在磁场中的运动时间t为 ![]() 及经过x轴的位置坐标值x0为
及经过x轴的位置坐标值x0为 ![]() .
.
【解析】(1)根据动能定理求得经电场加速后粒子的速度,再根据洛伦兹力提供圆周运动向心力求得粒子圆周运动的轨道半径;(2)粒子进入磁场做圆周运动,要使粒子不再经过x轴,则粒子离开磁场时速度方向与x轴平行,由比计算分析求解电场强度的取值范围;(3)根据几何关系求得粒子在磁场中圆周运动转过的圆心角,再根据周期求得在磁场中的运动时间,由几何关系求得粒子经过x轴的位置坐标.
【考点精析】解答此题的关键在于理解带电微粒(计重力)在电场中的运动的相关知识,掌握带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或明确的暗示以外,一般都不能忽略重力;由于带电粒子在匀强电场中所受电场力与重力都是恒力,因此可以用两种方法处理:①正交分解法;②等效“重力”法,以及对洛伦兹力的理解,了解洛伦兹力始终垂直于v的方向,所以洛伦兹力一定不做功.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】一群氢原子处于量子数n=4能级状态,氢原子的能级的示意图如图所示,则:
几种金属的逸出功
金属 | 铯 | 钙 | 镁 | 钛 |
选出功W/eV | 1.9 | 2.7 | 3.7 | 4.1 |

(1)氢原子可能发射几种频率的光子?
(2)氢原子由量子数n=4的能级跃迁到n=2的能级时辐射光子的能量是多少电子伏?
(3)用(2)中的光子照射下表中几种金属,哪些金属能发生光电 效应?发生光电效应时,发射光电子的最大初动能是多大?