题目内容
9. 一长木板置于光滑水平地面上,木板左端放置一小物块,在木板右方有一墙壁,木板右端与墙壁的距离为4m,如图(a)所示.t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1s时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1s时间内小物块的v-t图线如图(b)所示.小物块质量是木板质量的3倍,重力加速度大小g取10m/s2.求
一长木板置于光滑水平地面上,木板左端放置一小物块,在木板右方有一墙壁,木板右端与墙壁的距离为4m,如图(a)所示.t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1s时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1s时间内小物块的v-t图线如图(b)所示.小物块质量是木板质量的3倍,重力加速度大小g取10m/s2.求(1)木板与墙壁碰撞后,木板离开墙壁的最大距离;
(2)小物块距离木板左端的最终距离.
分析 (1)木板与墙壁碰撞后,木板和物块都在滑动摩擦力作用下做匀减速直线运动,根据b图求出物块的加速度,根据牛顿第二定律求出滑动摩擦力,从而求出木板的加速度,当木板速度减为零时,离墙壁最远,根据运动学基本公式求解最远距离;
(2)木板速度减为零后会在摩擦力作用下向右做匀加速运动,直到与木块速度相等,木板和物块系统动量守恒,每次物体都是与木板以相同的速度撞击墙壁,最终物块和木板一起停止在墙壁处,根据动能定理求解即可.
解答 解:(1)木板与墙壁碰撞后,在物块的滑动摩擦力作用下做匀减速直线运动,而木块在摩擦力作用下也做匀减速直线运动,根据b图可知,物块的加速度${a}_{1}=\frac{△{v}_{1}}{△{t}_{1}}=\frac{2-4}{1}=-2m/{s}^{2}$,
设木板的质量为m,则木块的质量为3m,
则摩擦力f=3ma1,
根据牛顿第二定律可知,木板的加速度${a}_{2}=\frac{f}{m}=\frac{3m×(-2)}{m}=-6m/{s}^{2}$,
当木板速度减为零时,离墙壁最远,则最远距离x=$\frac{{v}^{2}-{{v}_{0}}^{2}}{2{a}_{2}}=\frac{0-16}{2×(-6)}=1.33m$
(2)木板和物块系统动量守恒,每次物体都是与木板以相同的速度撞击墙壁,撞击后,木板速度大小不变,方向改变,此后系统动量守恒,最终物块和木板一起停止在墙壁处,
根据动能定理得:$\frac{1}{2}(m+3m){{v}_{0}}^{2}=fx$,
其中f的大小为f=-3ma1=6m,
解得x=$\frac{16}{3}m=5.33m$
答:(1)木板与墙壁碰撞后,木板离开墙壁的最大距离为1.33m;
(2)小物块距离木板左端的最终距离为5.33m.
点评 解决本题的关键理清木块和木板在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,第二问应用动量守恒定律及能量守恒定律较为简便,要注意正方向的规定,难度中等.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案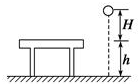 质量为m的小球从离桌面高度为H处由静止下落,桌面离地高度为h,如图所示.若以小球下落的初位置为参考平面,那么小球落地时的重力势能及整个过程中小球重力势能的变化分别为( )
质量为m的小球从离桌面高度为H处由静止下落,桌面离地高度为h,如图所示.若以小球下落的初位置为参考平面,那么小球落地时的重力势能及整个过程中小球重力势能的变化分别为( )| A. | mgH,减少mg(H-h) | B. | -mg(H+h),减少mg(H+h) | ||
| C. | -mgh,增加mg(H-h) | D. | mg(H-h),增加mg(H+h) |
| A. | 电容器所带的电荷越多,电容就越大 | |
| B. | 电容器两极板间的电压越高,电容就越大 | |
| C. | 电容器所带电荷量增加一倍,电容就越大 | |
| D. | 电容是描述电容器容纳电荷本领的物理量 |
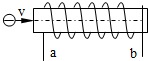 如图所示,一束电子以速度v沿管的轴一进入通电长直螺线管,忽略电子重力,电子在管内的运动应该是( )
如图所示,一束电子以速度v沿管的轴一进入通电长直螺线管,忽略电子重力,电子在管内的运动应该是( )| A. | 电子的速度逐渐减小 | B. | 电子的速度逐渐增大 | ||
| C. | 电子的速度方向改变 | D. | 电子做匀速直线运动 |
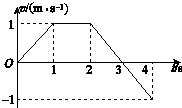
| A. | 第1s内和第3s内的运动方向相同 | B. | 第3s内和第4s内的加速度相同 | ||
| C. | 第1s内和第4s内的位移大小不相等 | D. | 0~2s和0~4s内的平均速度大小相等 |
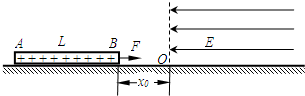 E,其方向为水平向左,BO距离为x0,若棒在水平向右的大小为$\frac{QE}{4}$的恒力作用下由静止开始运动.求:
E,其方向为水平向左,BO距离为x0,若棒在水平向右的大小为$\frac{QE}{4}$的恒力作用下由静止开始运动.求: