题目内容
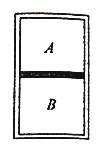
【题目】如图所示，可自由活动的活塞将密闭的气缸分为体积相等的上下两部分A和B ，初始时，A、B中密封的理想气体的温度均方800K，A中气体的压强为
，活塞质量m=2.5kg，气缸横截面积
，气缸和活塞都是由绝热材料制成的。现利用控制装置(未画出)保持A中气体的温度不变，缓慢降低B中气体的温度，使得B中气体的体积变为原来的
，若不计活塞与汽缸壁之间的摩擦，重力加速度取g=10m/s2。求稳定后B中气体的温度。
【答案】
【解析】
根据玻意耳定律求出A中气体末态的压强，根据活塞的受力平衡分别求出B中气体初末状态的压强，再对B中的气体运用理想气体状态方程即可求解稳定后B中气体的温度．
根据题意，B中气体的体积变为原来的
，则A中气体的体积以
变为原来体积
的
，即
，A中气体发生等温变化，根据玻意耳定律有
解得稳定后A中气体的压强
对B中气体，初态
末态
.
对B中气体，由理想气体状态方程有
解得.
练习册系列答案
相关题目
