Question

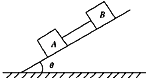
【题目】质量为50kg的空箱子放在光滑水平面上，箱子中有一同样质量的铁块，铁块与箱子的左壁相距10m，它一旦与左壁相碰将会瞬间粘在一起，然后不再分开，铁块与箱底的摩擦不计．用水平向右的推力10N作用于箱子，12s后立即去掉推力．求撤去推力瞬间箱子与铁块的共同速度．

Answer 1

【答案】解：箱子的加速度为：

a= =0.2m/s2，

根据s= 得箱子在通过10m的位移的时间为：

t= =10s，

所以10s后箱子与铁块相碰，

子与铁块碰撞前做匀加速运动，碰撞前的速度为：

v1=at=0.2×10m/s=2m/s．

设箱子与铁块碰撞后的速度为v2，由动量守恒定律得：

mv1=2mv2

代入数据解得：v2=1m/s．

推力作用剩余时间为：

t′=2s，

箱子和铁块的共同加速度为：

a′= = m/s2=0.1m/s2

则最终速度为：

v′=v2+a′t′=1+0.1×2m/s=1.2m/s．

答：撤去推力瞬间箱子与铁块的共同速度为1.2m/s．

【解析】根据牛顿第二定律求出箱子与铁块未碰撞前的加速度，结合位移时间公式求出箱子运动10m所需的时间，得出箱子碰撞前的速度，结合动量守恒求出碰撞后的共同速度，根据牛顿第二定律求出碰撞后整体的加速度，结合速度时间公式求出撤去拉力瞬间箱子与铁块的共同速度．
【考点精析】解答此题的关键在于理解动量守恒定律的相关知识，掌握动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．