题目内容
假若几年后中国人乘宇宙飞船探索月球并完成如下实验:①当飞船停留在距月球一定的距离时,正对着月球发出一个激光脉冲,经过时间t后收到反射回来的信号,并测得此刻月球对观察者眼睛的视角为θ;②当飞船在月球表面着陆后,科研人员在距月球表面h处以初速度v0水平抛出一个小球,并测出落点到抛出点的水平距离为s.已知万有引力常量为G,光速为c,月球的自转影响以及大气对物体的阻力均不计.试根据以上信息,求:
(1)月球的半径R;
(2)月球的质量M.
(1)月球的半径R;
(2)月球的质量M.
分析:(1)激光在真空中传播速度为c,由题意,激光脉冲经过时间t后收到反射回来的信号,则飞船到月球表面的距离为d=c?
t.作出视角示意图,由数学知识求月球的半径.
(2)根据万有引力等于重力,可列式求得月球表面的重力加速度与月球质量的关系.小球在月球表面做平抛运动的加速度就等于表面的重力加速度,根据平抛运动的规律求得重力加速度,联立即可求得月球的质量.
| 1 |
| 2 |
(2)根据万有引力等于重力,可列式求得月球表面的重力加速度与月球质量的关系.小球在月球表面做平抛运动的加速度就等于表面的重力加速度,根据平抛运动的规律求得重力加速度,联立即可求得月球的质量.
解答:解:(1)设飞船离月球表面的距离为d,由题意得
2d=ct
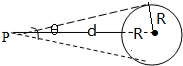 根据图示示意图,由几何知识得 R=(d+R)sin
根据图示示意图,由几何知识得 R=(d+R)sin
解得:R=
(2)设月球表面的重力加速度为g月,则
mg月=
得 g月=
小球做平抛运动,则有
h=
g月t2
s=v0t
联立解得:M=
答:
(1)月球的半径R为
;
(2)月球的质量M为
.
2d=ct
 根据图示示意图,由几何知识得 R=(d+R)sin
根据图示示意图,由几何知识得 R=(d+R)sin| θ |
| 2 |
解得:R=
ctsin
| ||
2(1-sin
|
(2)设月球表面的重力加速度为g月,则
mg月=
| GMm |
| R2 |
得 g月=
| GM |
| R2 |
小球做平抛运动,则有
h=
| 1 |
| 2 |
s=v0t
联立解得:M=
c2t2
| ||||
2Gs2(1-sin
|
答:
(1)月球的半径R为
ctsin
| ||
2(1-sin
|
(2)月球的质量M为
c2t2
| ||||
2Gs2(1-sin
|
点评:本题是几何知识、万有引力和平抛运动的综合,对于常见的抛体运动与万有引力的综合题,要抓住它们之间联系的纽带是重力加速度.根据万有引力等于重力,知道月球的半径和表面的重力加速度即可求得月球的质量.

练习册系列答案
相关题目