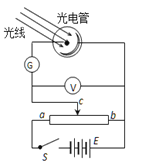
��Ŀ����
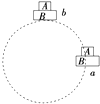
����Ŀ����ˮƽ��������ֱ�̶�һ���ڱڹ⻬��Բ�ܣ��ܵİ뾶R=3.6m���ܵ��ھ���С���Ժ��ԣ����ܵij���A��Բ�ĵ����Ϸ������B��Բ�ĵ���������ֱ�����60���ǣ���ͼ��ʾ������һֻ����m=1kg��С����Ϊ�ʵ㣩��ij��P��һ���ij��ٶ�ˮƽ�׳���ǡ�ôӹܿ�B�������߷�����룬С��Aʱǡ����ܱ�����������ȡg=10m/s2����
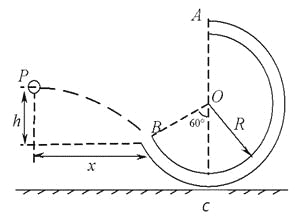
��1��С��Բ����ߵ�Aʱ���ٶȴ�С��
��2��С���ڹܵ���͵�Cʱ���ܱڶ�С��ĵ�����С��
��3��С���׳���P���ܿ�B��ˮƽ����x��
���𰸡���1��![]() ��2��
��2��![]() ��������ֱ���ϣ�3��
��������ֱ���ϣ�3��![]()
�������������������1��С�������ʱ�Թܱ���������������������ʽ��֪![]()
�ɵ�С��Բ����ߵ�ʱ���ٶ�![]()
��2������͵�C���ٶ�Ϊv��С��ӹܵ���͵㵽��ߵ�A���ɻ�е���غ㶨�ɿ�֪
![]() ���ɵ�
���ɵ�![]()
����͵㣬����������ʽ��֪![]()
�ɵ�![]()
��2����B����ٶ�ΪvB���ɻ�е���غ㶨�ɿ�֪![]()
�ɵ�![]()
��ƽ���˶����ɿ�֪��С����ƽ���˶����̵ij��ٶ�![]()
��B��ʱ����ֱ�ٶ�![]()
��![]() ��֪
��֪![]()
��![]() ��֪��С����׳��㵽�ܿ�B��ˮƽ����
��֪��С����׳��㵽�ܿ�B��ˮƽ����![]() m
m

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ