题目内容
7.物体万有引力场中具有的势能叫引力势能.取两物体相距无穷远时的引力势能为零.一个质量为m0的质点距离质量为M0的引力源中心为r0时,其引力势能EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$(式中G为引力常数).一颗质量为m的人造地球卫星以圆形轨道环绕地球飞行,已知地球的质量为M,由于受高空稀薄空气的阻力作用.卫星的圆轨道半径从r1逐渐减小到r2,若在这个过程中空气阻力做功为Wf,则在下面给出的Wf的四个表达式中正确是( )| A. | Wf=-GMm($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | B. | Wf=-$\frac{GMm}{2}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) | ||
| C. | Wf=-$\frac{GMm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | D. | Wf=-$\frac{2GMm}{3}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) |
分析 根据万有引力提供向心力求出卫星在半径为r1圆形轨道运动的速度,从而知道动能,通过引力势能公式求出在轨道r1上的机械能,同理可以求出卫星在轨道r2上的机械能,卫星的圆轨道半径从r1逐渐减小到r2.在这个过程中客服空气阻力做功Wf等于卫星机械能的减少.
解答 解:卫星在圆轨道半径从r1上时,根据万有引力提供向心力:$G\frac{Mm}{{{r}_{1}}^{2}}=m\frac{{{v}_{1}}^{2}}{{r}_{1}}$,解得${v}_{1}=\sqrt{\frac{GM}{{r}_{1}}}$,
所以${E}_{k1}=\frac{1}{2}m{{v}_{1}}^{2}=\frac{GMm}{2{r}_{1}}$,
卫星的总机械能:E1=Ek1+Ep1=$\frac{GMm}{2{r}_{1}}-\frac{GMm}{{r}_{1}}$=-$\frac{GMm}{2{r}_{1}}$,
同理:卫星的圆轨道半径从r2上时,${E}_{k2}=\frac{GMm}{2{r}_{2}}$,
卫星的总机械能:${E}_{2}=-\frac{GMm}{2{r}_{2}}$,
卫星的圆轨道半径从r1逐渐减小到r2.在这个过程中空气阻力做功为Wf,等于卫星机械能的减少:-Wf=E1-E2=$\frac{GMm}{2}(\frac{1}{{r}_{2}}-\frac{1}{{r}_{1}})$,则Wf=-$\frac{GMm}{2}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$).
故选:B.
点评 解决本题的关键得出卫星动能和势能的和即机械能的变化量,从而客服空气阻力做功为Wf等于卫星机械能的减少这个功能关系计算即可.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18.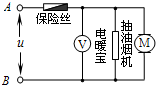 如图所示,电路中电源电压u=311sin100πt(V),A、B间接有“200V 440W”的电暖宝、“220V 220W“的抽油烟机、交流电压表及保险丝.下列说法正确的是( )
如图所示,电路中电源电压u=311sin100πt(V),A、B间接有“200V 440W”的电暖宝、“220V 220W“的抽油烟机、交流电压表及保险丝.下列说法正确的是( )
 如图所示,电路中电源电压u=311sin100πt(V),A、B间接有“200V 440W”的电暖宝、“220V 220W“的抽油烟机、交流电压表及保险丝.下列说法正确的是( )
如图所示,电路中电源电压u=311sin100πt(V),A、B间接有“200V 440W”的电暖宝、“220V 220W“的抽油烟机、交流电压表及保险丝.下列说法正确的是( )| A. | 此交流电的频率为100Hz | |
| B. | 抽油烟机1min消耗的电能为1.32×104J | |
| C. | 交流电压表的示数为311V | |
| D. | 电暖宝的发热功率是抽油烟机发热功率的2倍 |
2.下列说法正确的是( )
| A. | 用α粒子轰击氮${\;}_7^{14}N$原子核,产生了氧的同位素${\;}_8^{17}O$和一个质子 | |
| B. | 重核裂变释放大量能量,产生明显的质量亏损,所以反应后核子总数要减少 | |
| C. | 放射性同伴素因不改变其化学性质、半衰期短等优点被广泛作为示踪原子使用 | |
| D. | 根据玻尔理论可知,吸收能量的电子跃迁到更高能级后,核外电子的动能将减小 | |
| E. | 金属内的每个电子可以不断地吸收光子,当它积累的动能足够大时,就能逸出金属 |
12.下列说法中,符合物理学史的是( )
| A. | 伽利略根据理想斜面实验得出“力是维持物体运动的原因”这一结论 | |
| B. | 奥斯特发现了电流的磁效应,揭示了电和磁之间存在联系 | |
| C. | 牛顿发现了万有引力定律,库仑用扭秤实验测出了引力常量的数值 | |
| D. | 通电螺线管的磁场和条形磁铁的磁场相似,安培受此启发,提出了分子电流假说 |
17.图1所示为一列间谐横波在t=15秒时波形图,图2是这列波中P点的振动图线,那么该波的传播速度和传播方向是( )


| A. | v=50cm/s,向右传播 | B. | v=25cm/s,向左传播 | ||
| C. | v=50cm/s,向左传播 | D. | v=25cm/s,向右传播 |
 如图所示,长为31cm,内径均匀的细玻璃管开口向上竖直放置,管内水银柱的上端正好与管口齐平,封闭气体的长为10cm,温度为27℃,外界大气压强不变.若把玻璃管在竖直平面内缓慢转至开口竖直向下,这时留在管内的水银柱长为15cm,求:
如图所示,长为31cm,内径均匀的细玻璃管开口向上竖直放置,管内水银柱的上端正好与管口齐平,封闭气体的长为10cm,温度为27℃,外界大气压强不变.若把玻璃管在竖直平面内缓慢转至开口竖直向下,这时留在管内的水银柱长为15cm,求: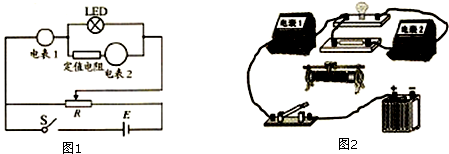

 1831年10月28日,法拉第在一次会议上展示了他发明的圆盘发电机,如图甲所示,这是人类历史上的第一台发电机.图乙是这个圆盘发电机的示意图:轻质圆形铜盘安装在水平铜轴上并与之垂直,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,使铜盘转动,阻值为R的电阻中就有电流通过.设铜盘转动的角速度为ω,铜盘半径为r,除R外其余电阻均不计,图示所示中磁场为磁感应强度大小为B、以过转轴的水平面为理想边界的匀强磁场,这个磁场只分布在过转轴的水平面以下的空间,不考虑摩擦和空气阻力.
1831年10月28日,法拉第在一次会议上展示了他发明的圆盘发电机,如图甲所示,这是人类历史上的第一台发电机.图乙是这个圆盘发电机的示意图:轻质圆形铜盘安装在水平铜轴上并与之垂直,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,使铜盘转动,阻值为R的电阻中就有电流通过.设铜盘转动的角速度为ω,铜盘半径为r,除R外其余电阻均不计,图示所示中磁场为磁感应强度大小为B、以过转轴的水平面为理想边界的匀强磁场,这个磁场只分布在过转轴的水平面以下的空间,不考虑摩擦和空气阻力.