题目内容
16. 1831年10月28日,法拉第在一次会议上展示了他发明的圆盘发电机,如图甲所示,这是人类历史上的第一台发电机.图乙是这个圆盘发电机的示意图:轻质圆形铜盘安装在水平铜轴上并与之垂直,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,使铜盘转动,阻值为R的电阻中就有电流通过.设铜盘转动的角速度为ω,铜盘半径为r,除R外其余电阻均不计,图示所示中磁场为磁感应强度大小为B、以过转轴的水平面为理想边界的匀强磁场,这个磁场只分布在过转轴的水平面以下的空间,不考虑摩擦和空气阻力.
1831年10月28日,法拉第在一次会议上展示了他发明的圆盘发电机,如图甲所示,这是人类历史上的第一台发电机.图乙是这个圆盘发电机的示意图:轻质圆形铜盘安装在水平铜轴上并与之垂直,它的边缘正好在两磁极之间,两块铜片C、D分别与转动轴和铜盘的边缘接触,使铜盘转动,阻值为R的电阻中就有电流通过.设铜盘转动的角速度为ω,铜盘半径为r,除R外其余电阻均不计,图示所示中磁场为磁感应强度大小为B、以过转轴的水平面为理想边界的匀强磁场,这个磁场只分布在过转轴的水平面以下的空间,不考虑摩擦和空气阻力.(1)求通过电阻R的电流大小和方向;
(2)要使铜盘匀速转动,需要对它施加外力的作用,求外力的功率.
分析 (1)由右手定则可明确电流的方向;根据转动切割产生的电动势公式可求得电动势,由欧姆定律求解电流的大小;
(2)根据功能关系可知,外力做功的功率等于电阻R的热功率;由电功率公式求解电功率即可.
解答 解:(1)由右手定则可知,流过电阻的电流方向向左;
铜盘转动产生的感应电动势相当于长度为r的金属杆绕其中一个端点匀速转动则产生电动势;即
E=$\frac{1}{2}$Bωr2
由欧姆定律可得:
I=$\frac{E}{R}$
解得:I=$\frac{B{ω}^{\;}{r}^{2}}{2R}$;
(2)铜盘转动过程中克服安培力所做的功等于产生的电能,电流做功把产生的电能全部又转化为焦耳热,所以外力做功的功率等于电阻R的热功率
即P=I2R
解得:P=$\frac{{B}^{2}{ω}^{2}{r}^{4}}{4R}$
答:(1)通过电阻R的电流大小$\frac{B{ω}^{\;}{r}^{2}}{2R}$;方向向左;(2)要使铜盘匀速转动,需要对它施加外力的作用,外力的功率为$\frac{{B}^{2}{ω}^{2}{r}^{4}}{4R}$.
点评 本题考查转动切割规律的应用,要求能熟记公式,并掌握电路规律,正确结合欧姆定律、电功等进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.物体万有引力场中具有的势能叫引力势能.取两物体相距无穷远时的引力势能为零.一个质量为m0的质点距离质量为M0的引力源中心为r0时,其引力势能EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$(式中G为引力常数).一颗质量为m的人造地球卫星以圆形轨道环绕地球飞行,已知地球的质量为M,由于受高空稀薄空气的阻力作用.卫星的圆轨道半径从r1逐渐减小到r2,若在这个过程中空气阻力做功为Wf,则在下面给出的Wf的四个表达式中正确是( )
| A. | Wf=-GMm($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | B. | Wf=-$\frac{GMm}{2}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) | ||
| C. | Wf=-$\frac{GMm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | D. | Wf=-$\frac{2GMm}{3}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) |
4.下列叙述中正确的是( )
| A. | 康普顿预言了中子的存在 | |
| B. | 在α粒子散射实验的基础上,卢瑟福提出了原子的核式结构模型 | |
| C. | 氡的半衰期为3.8天,若取4个氡原子核,经过7.6天后就一定只剩下一个氡原子核 | |
| D. | 一群处于n=4能级的氢原子回到n=2状态过程中,可能辐射3种不同频率的光子 |
11.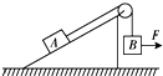 如图所示,顶端装有定滑轮的斜面体放置在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态,不计绳的质量和绳与滑轮间的摩擦.现用水平向右的拉力F作用于物体B上,将物体B缓慢拉高一定的距离,在此过程中斜面体与物体A仍然保持静止.关于此过程中,下列说法正确的是( )
如图所示,顶端装有定滑轮的斜面体放置在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态,不计绳的质量和绳与滑轮间的摩擦.现用水平向右的拉力F作用于物体B上,将物体B缓慢拉高一定的距离,在此过程中斜面体与物体A仍然保持静止.关于此过程中,下列说法正确的是( )
 如图所示,顶端装有定滑轮的斜面体放置在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态,不计绳的质量和绳与滑轮间的摩擦.现用水平向右的拉力F作用于物体B上,将物体B缓慢拉高一定的距离,在此过程中斜面体与物体A仍然保持静止.关于此过程中,下列说法正确的是( )
如图所示,顶端装有定滑轮的斜面体放置在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态,不计绳的质量和绳与滑轮间的摩擦.现用水平向右的拉力F作用于物体B上,将物体B缓慢拉高一定的距离,在此过程中斜面体与物体A仍然保持静止.关于此过程中,下列说法正确的是( )| A. | 斜面体对物体A的摩擦力一定增大 | B. | 地面对斜面体的支持力可能变大 | ||
| C. | 斜面体对物体A的摩擦力一定变大 | D. | 斜面体对物体A的作用力可能变大 |
5.在用如图示的实验装置做“碰撞中的动量守恒定律”实验中,下列说法正确的是( )


| A. | 斜糟轨道尽量光滑以减少误差 | |
| B. | 入射球和被碰球的质量必须相等,且大小相同 | |
| C. | 实验中不需要测量轨道末端离地面的高度 | |
| D. | 需要用圆规确定小球落地的平均位置,并用刻度尺测量落地水平距离 |
6. 如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )
如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )
 如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )
如图甲所示,质量不计的弹簧竖直固定在水平地面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹簧弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )| A. | t2时刻弹簧的弹性势能最大 | |
| B. | t3时刻弹簧的弹性势能最大 | |
| C. | t1~t3这段时间内,弹簧的弹性势能先减小后增加 | |
| D. | t1~t3这段时间内,弹簧的弹性势能先增加后减少 |
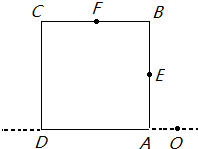 如图所示,空气中一透明柱体的横截面是边长为d的正方形ABCD,在DA边的延长线上距A点$\frac{{\sqrt{3}}}{6}d$处有一点光源O,发出一束单色光从AB边中点E进入介质后,经BC中点F射出,求:
如图所示,空气中一透明柱体的横截面是边长为d的正方形ABCD,在DA边的延长线上距A点$\frac{{\sqrt{3}}}{6}d$处有一点光源O,发出一束单色光从AB边中点E进入介质后,经BC中点F射出,求: