题目内容
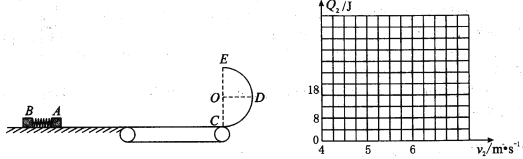
【题目】如图所示,水平地面上OP段是粗糙的,OP长为L=1.6m,滑块A、B与该段的动摩擦因数都为μ=0.5,水平地面的其余部分是光滑的.滑块B静止在O点,其质量mB=2kg.滑块A在O点左侧以v0=5m/s的水平初速度向右运动,并与B发生碰撞.A的质量是B的k(k取正整数)倍,滑块均可视为质点,取g=10m/s2
(1)若滑块A与B发生完全非弹性碰撞,求A、B碰撞过程中损失的机械能;
(2)若滑块A、B构成的系统在碰撞过程中没有机械能损失,试讨论k在不同取值范围时滑块A克服摩擦力所做的功。
![]()
【答案】(1)![]() (2)当k=1时WfA=0;当1<k≤9时WfA=
(2)当k=1时WfA=0;当1<k≤9时WfA=![]() ;当k>9时WfA=16 kJ
;当k>9时WfA=16 kJ
【解析】
(1)设滑块A碰B后的共同速度为v,A、B碰撞过程中损失的机械能为ΔE,由动量守恒定律有
mAv0=(mA+mB)v①
由能量守恒定律有
ΔE=![]() mA
mA![]() -
-![]() (mA+mB)v2②
(mA+mB)v2②
联立①②式并代入数据解得
ΔE=![]() J③
J③
(2)设碰撞后A、B速度分别为vA、vB,且设向右为正方向,由于弹性碰撞,有:
mAv0=mAvA+mBvB④
![]() mA
mA![]() =
=![]() mA
mA![]() +
+![]() mB
mB![]() ⑤
⑤
联立④⑤式并代入数据解得
vA=![]() m/s⑥
m/s⑥
vB=![]() m/s⑦
m/s⑦
假设滑块A、B都能在OP段滑动,滑块A、B在OP段的加速度(aA=aB=μg)相等,由⑥⑦式知在任意时刻vB>vA,滑块A、B不会再一次发生碰撞,由题知,当滑块A刚好能够到达P点有
![]() =μmAgL
=μmAgL
代入数据解得
k=9
讨论:
a.当k=1时,vA=0,滑块A停在O点,A克服摩擦力所做的功为WfA=0.
b.当1<k≤9时,滑块A停在OP之间,A克服摩擦力所做的功为
WfA=![]() =
=![]()
c.当k>9时,滑块A从OP段右侧离开,A克服摩擦力所做的功为
WfA=μmAgL=16kJ.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目