题目内容
1.已知地球的质量为M,地球的半径为R,地球的自转周期为T,地球表面的重力加速度为g,无线电信号的传播速度为c,如果你用卫星电话通过地球同步卫星中的转发器转发的无线电信与对方通话,则在你讲完话后听到对方的回话所需的最短时间为$\frac{4}{c}$($\root{3}{\frac{g{R}^{2}{T}^{2}}{4π}}$-R).分析 同步卫星和月球都是绕地球做匀速圆周运动,根据万有引力提供向心力$\frac{GMm}{{r}^{2}}$=mr$\frac{4{π}^{2}}{{T}^{2}}$,求出轨道半径,从而得出同步卫星的高度,根据速度公式求出时间.
解答 解:地球同步卫星是相对地面静止的卫星,它绕地球运动的周期与地球自转周期T相同.
设卫星距地面的距离h,卫星绕地球做匀速圆周运动的向心力是地球对卫星的万有引力,
由牛顿运动定律和万有引力定律,可得:G$\frac{Mm}{(R+h)^{2}}$=m(R+h)($\frac{2π}{T}$)2
解得:h=$\root{3}{\frac{GM{T}^{2}}{4π}}$-R
信号传递的最短距离是2 h,受话人听到发话人的信号后立即回话,信号又需传播2 h的距离后才能到达发话人处,
由此可知最短时间为:t=$\frac{2×2h}{c}$=$\frac{4}{c}$•($\root{3}{\frac{GM{T}^{2}}{4π}}$-R)
根据黄金代换得:GM=gR2,
t=$\frac{4}{c}$($\root{3}{\frac{g{R}^{2}{T}^{2}}{4π}}$-R)
故答案为:$\frac{4}{c}$($\root{3}{\frac{g{R}^{2}{T}^{2}}{4π}}$-R).
点评 解决本题的关键掌握万有引力提供向心力$\frac{GMm}{{r}^{2}}$=mr$\frac{4{π}^{2}}{{T}^{2}}$,并掌握向心力表达式的内容,注意黄金代换公式:GM=gR2的作用.

练习册系列答案
相关题目
9. 如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断错误的是( )
如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断错误的是( )
 如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断错误的是( )
如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为1.0×105N,此时千斤顶两臂间的夹角为120°,则下列判断错误的是( )| A. | 此时两臂受到的压力大小均为2.0×105N | |
| B. | 此时千斤顶对汽车的支持力为1.0×105N | |
| C. | 若继续摇动手把,两臂受到的压力将增大 | |
| D. | 若继续摇动手把,两臂受到的压力将减小 |
6.如果带电粒子进入电场时的速度与匀强电场的电场力垂直,则粒子在电场中做类平抛运动,若不计粒子的重力,影响粒子通过匀强电场时间的因素是( )
| A. | 粒子的带电荷量 | B. | 粒子的初速度 | C. | 粒子的质量 | D. | 粒子的加速度 |
13. 如图所示,质量为m的小球(可看做质点),在竖直放置的半径为R的固定光滑圆环轨道内运动,若小球通过最高点时的速率为v0=$\sqrt{gR}$,下列说法中正确的是( )
如图所示,质量为m的小球(可看做质点),在竖直放置的半径为R的固定光滑圆环轨道内运动,若小球通过最高点时的速率为v0=$\sqrt{gR}$,下列说法中正确的是( )
 如图所示,质量为m的小球(可看做质点),在竖直放置的半径为R的固定光滑圆环轨道内运动,若小球通过最高点时的速率为v0=$\sqrt{gR}$,下列说法中正确的是( )
如图所示,质量为m的小球(可看做质点),在竖直放置的半径为R的固定光滑圆环轨道内运动,若小球通过最高点时的速率为v0=$\sqrt{gR}$,下列说法中正确的是( )| A. | 小球在最高点时只受重力作用 | |
| B. | 小球在最高点对圆环的压力大小为mg | |
| C. | 小球在最高点时重力的瞬时速率为0 | |
| D. | 小球在绕圆环运动一周的时间大于$\frac{2πR}{{v}_{0}}$ |
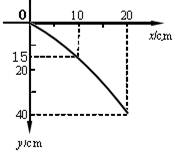 某学生在做“研究平抛运动”的实验中,忘记记下小球做平抛运动的起点位置,如图0点为物体运动一段时间后的位置,取为坐标原点,根据轨迹的坐标求出物体做平抛运动的初速度为V0=1m/s m/s(g=10m/s2);求出抛出点的坐标为B(填入正确的序号).
某学生在做“研究平抛运动”的实验中,忘记记下小球做平抛运动的起点位置,如图0点为物体运动一段时间后的位置,取为坐标原点,根据轨迹的坐标求出物体做平抛运动的初速度为V0=1m/s m/s(g=10m/s2);求出抛出点的坐标为B(填入正确的序号).