题目内容
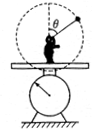 如图所示,一质量为M的人站在台秤上,手拿一个质量为m、悬线长为R的小球(其中M>m),在竖直平面内使小球做圆周运动,且小球恰好能通过圆轨道的最高点.求:
如图所示,一质量为M的人站在台秤上,手拿一个质量为m、悬线长为R的小球(其中M>m),在竖直平面内使小球做圆周运动,且小球恰好能通过圆轨道的最高点.求:(1)小球在圆周运动过程中的最大速度;
(2)台秤示数的最大值;
(3)台秤示数的最小值.
分析:知道小球恰好能通过圆轨道的最高点的临界条件.
小球运动到最低点时悬线对人的拉力最大,且方向竖直向下,故台秤示数最大,
根据机械能守恒和牛顿第二定律求出拉力在竖直方向的最小值.
小球运动到最低点时悬线对人的拉力最大,且方向竖直向下,故台秤示数最大,
根据机械能守恒和牛顿第二定律求出拉力在竖直方向的最小值.
解答:解:(1)小球恰好能通过圆轨道的最高点,由机械能守恒及牛顿第二定律有:
mg=m
其中υ0表示小球在圆轨道最高点时的速度
=
+2mgR
由此得小球通过最低点时的速度,亦即最大速度为 υ=
(2)小球运动到最低点时悬线对人的拉力最大,且方向竖直向下,故台秤示数最大,
小球通过最低点时,据牛顿第二定律有T-mg=
解得T=6mg
所以台秤的最大示数为F=(M+6m)g
(3)当小球处于如图所示状态时,
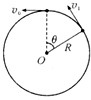
设其速度为v1,由机械能守恒有
=
+mgR(1-cosθ)
由牛顿第二定律有:T+mgcosθ=
解得悬线拉力 T=3mg(1-cosθ)
其分力Ty=Tcosθ=3mgcosθ-3mgcos2θ
当cosθ=
,即θ=60°时,
台秤的最小示数为Fmin=Mg-Ty=Mg-
mg.
mg=m
| ||
| R |
| mυ2 |
| 2 |
| mυ02 |
| 2 |
由此得小球通过最低点时的速度,亦即最大速度为 υ=
| 5gR |
(2)小球运动到最低点时悬线对人的拉力最大,且方向竖直向下,故台秤示数最大,
小球通过最低点时,据牛顿第二定律有T-mg=
| mυ2 |
| R |
解得T=6mg
所以台秤的最大示数为F=(M+6m)g
(3)当小球处于如图所示状态时,

设其速度为v1,由机械能守恒有
| mυ12 |
| 2 |
| mυ02 |
| 2 |
由牛顿第二定律有:T+mgcosθ=
| mυ12 |
| R |
解得悬线拉力 T=3mg(1-cosθ)
其分力Ty=Tcosθ=3mgcosθ-3mgcos2θ
当cosθ=
| 1 |
| 2 |
台秤的最小示数为Fmin=Mg-Ty=Mg-
| 3 |
| 4 |
点评:对物体进行受力分析,运用牛顿第二定律列出力与力的关系,根据题目的条件中找到临界状态.
对于圆周运动的受力问题,我们要找出向心力的来源.
对于圆周运动的受力问题,我们要找出向心力的来源.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为
如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为 如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2
如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2 如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( )
如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( ) 如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( )
如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( ) 如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.
如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.