题目内容
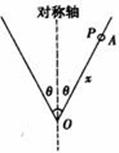
 如图所示,将一根光滑的细金属棒折成V形,顶角为2θ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,
如图所示,将一根光滑的细金属棒折成V形,顶角为2θ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,(1)若固定V形细金属棒,小金属环P从距离顶点O为x的A点处由静止自由滑下,则小金属环由静止下滑至顶点O点时需多少时间?
(2)若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动时,则小金属环离对称轴的距离为多少?
分析:(1)先根据牛顿第二定律求出金属球下滑的加速度,再根据匀加速直线运动位移时间公式即可求解;
(2)若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动,合外力提供向心力,根据向心力公式求出半径.
(2)若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动,合外力提供向心力,根据向心力公式求出半径.
解答:解:(1)对金属球进行受力分析根据牛顿第二定律得:
a=
=gcosθ
金属球下滑做匀加速运动,则有:
x=
at2
解得:t=
(2)金属球做匀速圆周运动,根据向心力公式得:mgcotθ=mω2r,
而ω=2πn
解得:r=
答:(1)小金属环由静止下滑至顶点O点的时间为
;
(2)小金属环离对称轴的距离为
.
a=
| mgcosθ |
| m |
金属球下滑做匀加速运动,则有:
x=
| 1 |
| 2 |
解得:t=
|
(2)金属球做匀速圆周运动,根据向心力公式得:mgcotθ=mω2r,
而ω=2πn
解得:r=
| gcotθ |
| 4π2n2 |
答:(1)小金属环由静止下滑至顶点O点的时间为
|
(2)小金属环离对称轴的距离为
| gcotθ |
| 4π2n2 |
点评:本题主要考查了牛顿第二定律及匀速圆周向心力公式的直接应用,关键是对小球进行受力分析求出合力,难度不大,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 如图所示,将一根光滑的细金属棒折成V形,顶角为2θ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,若小金属环P随V形细金属棒绕其对称轴以角速度ω匀速转动时,小金属环与棒保持相对静止,则小金属环离对称轴的距离为多少?
如图所示,将一根光滑的细金属棒折成V形,顶角为2θ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,若小金属环P随V形细金属棒绕其对称轴以角速度ω匀速转动时,小金属环与棒保持相对静止,则小金属环离对称轴的距离为多少? ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P.
,其对称轴竖直,在其中一边套上一个质量为m的小金属环P.
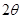 ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P.
,其对称轴竖直,在其中一边套上一个质量为m的小金属环P.