题目内容
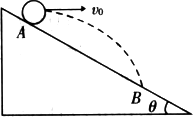
在一个倾角为θ的斜面上的A点将一小球以初速度v0平抛出去，最后落在斜面上的B点，如图所示．求物体的飞行时间及小球离斜面的最远距离．
答案：
解析：
解析：
|
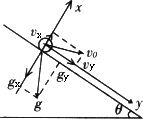
解析：建立如图所示坐标系，将v0及g分解到x和y方向上有： vx＝vxsinθ，vy＝v0cosθ， gx＝gcosθ，gy＝gsinθ． 可见，在x方向上，小球以vx为初速度，以gx为加速度做匀减速直线运动，在该方向上速度减小到零时小球离斜面最远．设此过程历时为t1，则有： t1＝vx/gx＝v0sinθ/gcosθ＝v0tanθ/g． 由对称性可知小球从最远点再回到斜面上历时也为t1，故小球飞行时间为t＝2t1＝2v0tanθ/g．最远距离xmax＝v0sinθ)2/2gcosθ＝
|
θcosθ/2g．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一质量为m的物体以某一速度冲上一个倾角为37°的斜面，其运动的加速度的大小为0.9g，这个物体沿斜面上升的最大高度为H，则在这过程中（ ）
一个倾角为θ=37°的斜面固定在水平面上，一个质量为m=1.0kg的小物块（可视为质点）以v0=4.0m/s的初速度由底端沿斜面上滑，小物块与斜面的动摩擦因数μ=0.25．若斜面足够长，已知sin37°=0.6，cos37°=0.8，g取10m/s2，求：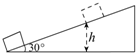
如图所示，一质量为m的物体以某一速度冲上一个倾角为30° 的斜面，其运动的加速度为
（2010?上海二模）如图所示，在磁感应强度大小为B的匀强磁场中，两条足够长的平行导轨组成一个倾角为53°的斜面框架，磁场方向与导轨所在平面垂直．导轨上端连接一阻值为2R的电阻和电键S，导轨电阻不计．两金属棒a和b的电阻均为R，质量分别为ma=0.05kg和mb=0.02kg，它们与导轨接触良好，并可沿导轨无摩擦地运动，g取10m/s2，sin53°=0.8，cos53°=0.6．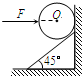
一个倾角为45°的斜面固定于竖直墙上，为使质量分布均匀的光滑铁球静止在如图所示的位置，需用一个水平推力F作用于球体上，F的作用线通过球心．设球体的重力为G，竖直墙对球体的弹力为N1，斜面对球体的弹力为N2，则以下结论正确的是（ ）